2022-2023学年广东深圳罗湖区七年级上册期中数学试卷及答案
一、选择题(本大题共10小题,共30.0分.在每小题列出的选项中,选出符合题目的一项)
1. 用一个平面去截一个几何体,截面不可能是圆的几何体的是()
A. 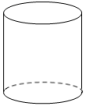 B.
B. 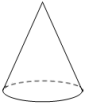 C.
C.  D.
D. 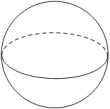
【答案】C
2. -5的相反数是( )
A. ![]() B.
B. ![]() C. 5 D. -5
C. 5 D. -5
【答案】C
3. 在﹣4,2,﹣1,3这四个数中,比﹣2小的数是( )
A. ﹣4 B. 2 C. ﹣1 D. 3
【答案】A
4. 下列说法中,正确的是()
A. 在有理数中,零的意义表示没有
B. 正有理数和负有理数组成全体有理数
C. 0.7既不是整数也不是分数,因此它不是有理数
D. 0是最小的非负整数,它既不是正数,也不是负数
【答案】D
5. 下列哪个图形是正方体的展开图()
A. 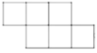 B.
B. 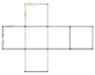 C.
C. 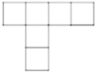 D.
D. 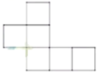
【答案】B
6. 温度由﹣4℃上升7℃是( )
A. 3℃ B. ﹣3℃ C. 11℃ D. ﹣11℃
【答案】A
7. 若数轴上表示-1和3的两点分别是点A和点B,则点A和点B之间的距离是()
A. -4 B. -2 C. 2 D. 4
【答案】D
8. 下面形状的四张纸板,按图中线经过折叠可以围成一个直三棱柱的是()
A. 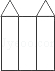 B.
B.  C.
C.  D.
D. 
【答案】C
9. 如图所示,是一个正方体纸盒的展开图,若在其中的三个正方形A,B,C分别填入适当的数,使得它们折成正方体后相对面上的两个数互为相反数,则填入正方形A,B,C的三个数依次为( )
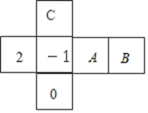
A. 1,﹣2,0 B. ﹣2,1,0 C. ﹣2,0,1 D. 0,﹣2,1
【答案】B
10. 式子|x﹣1|-3取最小值时,x等于( )
A. 1 B. 2 C. 3 D. 4
【答案】A
二、填空题(本大题共5小题,共15.0分)
11. 如果规定盈利为正,那么亏损500元记作____________元.
【答案】![]()
12. 一个棱柱有![]() 个面,则这个棱柱的底面是______边形.
个面,则这个棱柱的底面是______边形.
【答案】八##8
13. 某年级举办足球循环赛,规则是:胜一场得3分,平一场得1分,输一场得-1分.某班的比赛结果是胜3场、平2场、输4场,则该班得________分.
【答案】7
14. 在数轴上,与表示-1的点的距离为3个单位长度的点所表示的数是___________.
【答案】![]() 或2
或2
15. 若|x|=4,|y|=5,则x-y的值为____________.
【答案】±1,±9
三、解答题(本大题共7小题,共55.0分.解答应写出文字说明,证明过程或演算步骤)
16. 计算:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() .
.
【答案】(1)![]()
(2)12(3)![]()
【分析】(1)利用有理数的加减运算的法则进行求解即可;
(2)利用乘法分配律进行运算即可;
(3)先计算乘方和绝对值,然后计算乘除,最后计算加减.
【小问1详解】
解:原式![]() ;
;
【小问2详解】
解:原式![]() ;
;
【小问3详解】
解:原式![]() .
.
17. 已知a,b互为相反数,m,n互为倒数,c的绝对值为2,求代数式![]() 的值.
的值.
【答案】-1或3
【分析】根据互为相反数的两数之和为0,互为倒数的两数之积为1,绝对值为2的数为2或﹣2,得到关系式,代入所求式子中计算即可求出值.
【详解】根据题意得:a+b=0,mn=1,c=2或﹣2.
①当c=2时,原式=0+1﹣2=-1;
②当c=﹣2时,原式=0+1+2=3.
综上所述:![]() 的值为-1或3.
的值为-1或3.
18. 如图是一个几何体从三个方向看所得到的形状图.
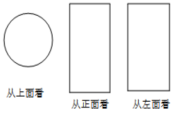
(1)写出这个几何体的名称;
(2)若从正面看的长为![]() ,从上面看到的圆的直径为
,从上面看到的圆的直径为![]() ,求这个几何体的表面积(结果保留
,求这个几何体的表面积(结果保留![]() ).
).
【答案】(1)圆柱;(2)![]() .
.
【分析】(1)根据该几何体的主视图与左视图是矩形,俯视图是圆可以确定该几何体是圆柱;
(2)根据告诉的几何体的尺寸确定该几何体的表面积即可;
【详解】(1)由三视图判断出该几何体是圆柱.
(2![]() ∵从正面看的长为
∵从正面看的长为![]() ,从上面看的圆的直径为
,从上面看的圆的直径为![]() ,
,
∴该圆柱的底面半径径为![]() ,高为
,高为![]() ,
,
∴该几何体的侧面积为![]() ,底面积为:2πr2=8πcm2.
,底面积为:2πr2=8πcm2.
∴该几何体的表面积为![]() .
.
19. 先化简,再求值:![]() ,其中
,其中![]() ,b=2.
,b=2.
【答案】![]() ,原式=13.
,原式=13.
【分析】首先利用去括号法则对整式化简,再合并同类项,接下来将a、b的值代入计算即可求得答案.
【详解】解:原式=![]()
=![]()
将![]() ,b=2代入
,b=2代入
原式=![]()
=13.
20. 我们定义一种新运算:a*b=a2﹣b+ab.例如:1*3=12﹣3+1×3=1.
(1)求2*(﹣3)的值.
(2)求(﹣2)*[2*(﹣3)]的值.
【答案】(1)1;(2)1.
【详解】试题分析:(1)根据新运算的定义式a*b=a2-b+ab,代入数据即可算出结论;
(2)根据(1)可知2*(-3)=1,再根据新运算的定义式a*b=a2-b+ab,代入数据即可算出结论.
试题解析:解:(1)2*(﹣3)=22﹣(﹣3)+2×(﹣3)=4+3﹣6=1;
(2)(﹣2)*[2*(﹣3)]=(﹣2)*1=(﹣2)2﹣1+(﹣2)×1=4﹣1﹣2=1.
21. 一位出租车司机某日中午的营运全在市区的环城公路上进行.如果规定:顺时针方向为正,逆时针方向为负,那天中午他拉了五位乘客所行车的里程如下:(单位:千米)+10,﹣7,+4,﹣9,+2.
(1)将最后一名乘客送到目的地时,这位司机距离出车地点的位置如何?
(2)若汽车耗油为![]() 升/千米,那么这天中午这辆出租车的油耗多少升?
升/千米,那么这天中午这辆出租车的油耗多少升?
(3)如果出租车的收费标准是:起步价10元,3千米后每千米2元,问:这个司机这天中午的收入是多少?
【答案】(1)0,回到起点(2)32a升;(3)86元
【分析】(1)计算这位司机行驶的路程的代数和即可,
(2)计算出每段路程的绝对值的和后乘以a,即为这天中午汽车共耗油数;
(3)表示出每段的收入后计算它们的和即为中午的收入.
【详解】(1)+10+(﹣7)+4+(﹣9)+2=0,
答:这位司机回到起点;
(2)|10|+|-7|+|+4|+|-9|+|+2|=32,
32×a=32a(升)
答:这天中午这辆出租车的油耗32a升;
(3)(10-3)×2+10+(7-3)×2+10+(4-3)×2+10+(9-3)×2+10+10=86(元)
答:这个司机这天中午的收入是86元
22. 阅读下列内容:![]() ,
,![]() ,
,![]() ,
,![]()
根据观察到的规律解决以下问题:
(1)第![]() 个等式是______;
个等式是______;
(2)若![]() 是正整数,则第
是正整数,则第![]() 个等式是______;
个等式是______;
(3)计算:![]() .
.
【答案】(1)![]()
(2)![]()
(3)![]()
【分析】(1)观察给出的式子可以发现:等式左边的分子全是1,分母依次是![]() ,
,![]() ,
,![]() 所以第5个等式的左边就是
所以第5个等式的左边就是![]() ,等式右边依次是
,等式右边依次是![]() ,
,![]() ,
,![]() ,所以第5个等式的右边是
,所以第5个等式的右边是![]() ;
;
(2)根据第(1)小问的分析即可得出第n个式子的左边为![]() ,右边为
,右边为![]() ;
;
(3)将![]() ,
,![]() ,
,![]() ,
,![]() ,…
,…![]() 按照找出
按照找出![]() 规律进行转换再相加即可得结果.
规律进行转换再相加即可得结果.
【小问1详解】
解:∵第1个式子:![]()
第2个式子:![]()
第3个式子∶![]()
∴第4个式子:![]()
∴第5个式子:![]() ;
;
故答案为:![]()
【小问2详解】
解:由第(1)问可知:第n个式子:![]()
【小问3详解】
解:![]()
![]()
![]()
![]()
![]()