2022-2023学年广东深圳龙岗区七年级上册期末数学试卷及答案
一、选择题:(每道题只有一个正确选项,请将答题卡上的正确选项涂黑,每小题3分,共30分)
1. 龙岗某校七年级(1)班期末考试数学的平均成绩是73分,小亮得了90分,记作![]() 分,若小英的成绩记作
分,若小英的成绩记作![]() 分,表示小英得了()分.
分,表示小英得了()分.
A. 76 B. 73 C. 77 D. 70
【答案】D
2. 2022年11月5日,第23届深圳读书月正式启动,本次读书月以“读时代新篇,创文明典范”为主题,按照文明的阶梯、文化的闹钟、城市的雅集、阅读的节日四大板块,设置了科学、人文、艺术三大专场,深圳读书月自创办以来,累计吸引![]() 亿人次参与,将数据
亿人次参与,将数据![]() 亿(240000000)用科学记数法表示为()
亿(240000000)用科学记数法表示为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
3. 下列是正方体展开图的是( )
A. 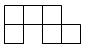 B.
B. 
C. 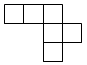 D.
D. 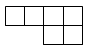
【答案】B
4. 若单项式![]() 与
与![]() 是同类项,则
是同类项,则![]() 的值是()
的值是()
A. ![]() B.
B. ![]() C. 9 D. 4
C. 9 D. 4
【答案】B
5. 如果![]() 是关于
是关于![]() 的方程
的方程![]() 的解,则
的解,则![]() 的值为()
的值为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
6. 下列计算正确的是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
7. 如图,点O在直线![]() 上,射线
上,射线![]() 是
是![]() 的平分线,若
的平分线,若![]() ,则
,则![]() 的度数是()
的度数是()
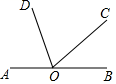
A. 20° B. 45° C. 60° D. 70°
【答案】D
8. 有理数a,b在数轴上对应的位置如图所示,则( )
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】C
9. “鸡兔同笼”问题是中国古代著名典型趣题之一,大约在1500年前,《孙子算经》中就记载了这个有趣的问题:今有雄(鸡)兔同笼,上有三十五头,下有九十四足,问雉兔各几何?这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头,从下面数,有94只脚.问笼中各有多少只鸡和兔?如果我们设有x只鸡,则可列方程()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
10. 如图所示,动点![]() 从第一个数
从第一个数![]() 的位置出发,每次跳动一个单位长度,第一次跳动一个单位长度到达数
的位置出发,每次跳动一个单位长度,第一次跳动一个单位长度到达数![]() 的位置,第二次跳动一个单位长度到达数
的位置,第二次跳动一个单位长度到达数![]() 的位置,第三次跳动一个单位长度到达数
的位置,第三次跳动一个单位长度到达数![]() 的位置,…,依此规律跳动下去,点
的位置,…,依此规律跳动下去,点![]() 从
从![]() 跳动
跳动![]() 次到达
次到达![]() 的位置,点点
的位置,点点![]() 从
从![]() 跳动
跳动![]() 次到达
次到达![]() 的位置,…,点
的位置,…,点![]() 在一条直线上,则点
在一条直线上,则点![]() 从
从![]() 跳动()次可到达
跳动()次可到达![]() 的位置.
的位置.
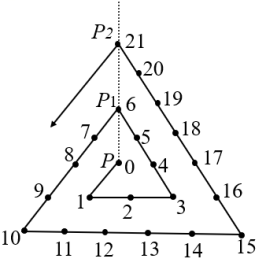
A. 595 B. 666 C. 630 D. 703
【答案】B
第Ⅱ卷(非选择题)
二、填空题:(本大题共5小题,每题3分,共15分)
11. 单项式![]() 的系数为__________.
的系数为__________.
【答案】![]() ##
##![]()
12. 如图所示的网格式正方形网格,∠ABC________∠DEF(填“>”,“=”或“<”)
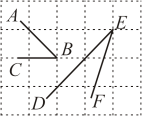
【答案】>
13. 如图,已知线段![]() ,点C在线段
,点C在线段![]() 上,
上,![]() ,则
,则![]() __________
__________![]() .
.
![]()
【答案】4
14. 2022年11月13日,全球首个“国际红树林中心”落地深圳,为了解学生对红树林生态系统的认知水平,龙岗区某校对初中部1200名学生进行了红树林生态系统知识测试,并从中抽取了100名学生的成绩进行统计分析,下列说法正确的是__________.(填序号)
①1200名学生是总体;②100名学生![]() 测试成绩是总体的一个样本;
测试成绩是总体的一个样本;
③样本容量是100名学生;④该校初中部每个学生的测试成绩是个体.
【答案】④
15. 龙岗某校积极响应“双减”政策,开展课后延时服务,七年级某数学兴趣小组在课后综合实践活动中,把一个直角三角尺![]() 的直角顶点O放在互相垂直的两条直线
的直角顶点O放在互相垂直的两条直线![]() 的垂足O处,并使两条直角边落在直线
的垂足O处,并使两条直角边落在直线![]() 上,若将
上,若将![]() 绕着点O顺时针旋转一个小于
绕着点O顺时针旋转一个小于![]() 的角得到
的角得到![]() ,射线
,射线![]() 是
是![]() 的角平分线且满足
的角平分线且满足![]() ,则
,则![]() __________.
__________.
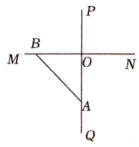
【答案】![]() 或
或![]()
三、解答题(共7题,55分)
16. 计算:
(1)![]()
(2)![]()
【答案】(1)![]()
(2)![]()
【小问1详解】
解:原式![]()
![]() .
.
【小问2详解】
解:原式![]()
![]()
![]()
![]() .
.
17. (1)化简:![]() ;
;
(2)先化简再求值:![]() ,其中
,其中![]() .
.
【答案】(1)![]() ,(2)
,(2)![]() ,
,![]()
【分析】(1)先去括号,再按照整式的加减混合运算计算即可;
(2)先去括号,再按照整式的加减混合运算化简,最后将a和b的值带入求解即可.
【详解】解:(1)原式![]()
![]() .
.
(2)原式![]()
![]()
![]() ,
,
当![]() 时,
时,
原式![]()
![]()
![]() .
.
18. 解方程:
(1)![]()
(2)![]()
【答案】(1)![]()
(2)![]()
【分析】(1)去括号,合并同类项,移项,系数化为![]() ,即可求解;
,即可求解;
(2)去分母,移项,合并同类项,系数化为![]() ,即可求解.
,即可求解.
【小问1详解】
解:![]()
![]()
![]()
![]() ,
,
∴原方程的解为![]() .
.
【小问2详解】
解:![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
∴原方程的解是![]() .
.
19. 如图,已知线![]() 、
、![]() ,求作一条线段
,求作一条线段![]() ,使
,使![]() .
.
要求:不写画法,保留必要的作图痕迹.
![]()
【答案】作图见详解
【分析】画射线![]() ,用尺规在射线
,用尺规在射线![]() 上取
上取![]() ,取
,取![]() ,再以
,再以![]() 点为起点,向反方向取
点为起点,向反方向取![]() ,则
,则![]() 即为所求线段
即为所求线段![]() .
.
【详解】解:如图如下,
![]()
![]() ,
,![]() ,以
,以![]() 点为起点,向反方向,即
点为起点,向反方向,即![]() 方向取
方向取![]() ,
,
∴![]() .
.
20. 为贯彻落实习近平总书记关于教育、体育的重要论述,深圳市教育局于日前发布《深圳市全面加强和改进新时代学校体育工作的实施意见》并面向社会公开征求意见,某校在七年级学生中随机抽取了若干名学生参加“平均每天体育运动时间”的调查,根据调查数据进行收集、整理描述和分析,下面给出了部分信息:
![]() .“平均每天体育运动时间”的不完全频数分布图:(数据分成五组:
.“平均每天体育运动时间”的不完全频数分布图:(数据分成五组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
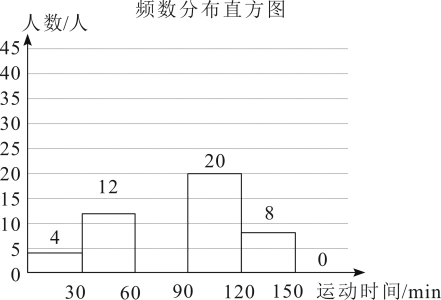
![]() .“平均每天体育运动时间”在
.“平均每天体育运动时间”在![]() 这一组的是:
这一组的是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
![]() .“平均每天体育运动时间”在
.“平均每天体育运动时间”在![]() 这一组的频率是
这一组的频率是![]() ;
;
![]() .小明的“平均每天体育运动时间”是
.小明的“平均每天体育运动时间”是![]() 分钟.
分钟.
请根据以上信息,解答下列问题:
(1)本次调查一共调查了______人;
(2)小明的“平均每天体育运动时间”在所有被调查人中排第_______(按从低到高排序);
(3)请补全频数分布直方图;
(4)若该校七年级共有![]() 名学生,试估计该校七年级学生平均每天体育运动时间低于
名学生,试估计该校七年级学生平均每天体育运动时间低于![]() 学生人数.
学生人数.
【答案】(1)![]()
(2)![]()
(3)![]() 的人数为
的人数为![]() 人,补全频数分布直方图见详解
人,补全频数分布直方图见详解
(4)![]() 人
人
【分析】(1)根据“平均每天体育运动时间”在![]() 这一组的频率是
这一组的频率是![]() ,即可求出本次调查一共调查的人数;
,即可求出本次调查一共调查的人数;
(2)![]() 的有
的有![]() 人,
人,![]() 的有
的有![]() 人,小明是
人,小明是![]() 分钟,即可求解;
分钟,即可求解;
(3)![]() 的人数是总人数分别减去
的人数是总人数分别减去![]() ,
,![]() ,
,![]() ,
,![]() 的人数,求出人数后即可补全频数分布直方图;
的人数,求出人数后即可补全频数分布直方图;
(4)运动时间低于![]() 的频数为
的频数为![]() ,用
,用![]() 人乘以这个频率即可求解.
人乘以这个频率即可求解.
【小问1详解】
解:![]() (人),即本次一共调查了
(人),即本次一共调查了![]() 人,
人,
故答案为:![]() .
.
![]() 小问2详解】
小问2详解】
解:![]() 的有
的有![]() 人,
人,![]() 的有
的有![]() 人,小明的时间是
人,小明的时间是![]() 分钟,则从低到高的排序是:
分钟,则从低到高的排序是:![]() 的有
的有![]() 人,
人,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (小明),
(小明),![]() ,
,
∴小明的“平均每天体育运动时间”在所有被调查人中排第名为:![]() ,即第
,即第![]() 名.
名.
【小问3详解】
解:![]() 的人数为:
的人数为:![]() (人),补全频数分布直方图,如图所示,
(人),补全频数分布直方图,如图所示,
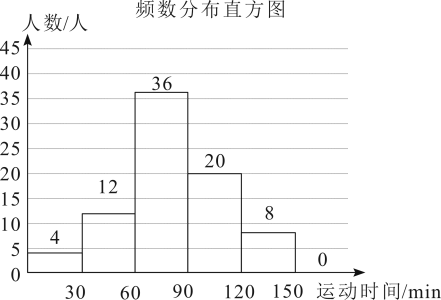
∴![]() 的人数为
的人数为![]() 人.
人.
【小问4详解】
解:![]() (人),
(人),
∴该校七年级学生平均每天体育运动时间低于![]() 学生人数约为
学生人数约为![]() 人.
人.
21. “我没有带你去感受过十月田间吹过的微风,如智者一般的谷穗,我没有带你去见证过这一切,但是亲爱的,我可以让你品尝这样的大米,”这是“东方甄选”带货王董宇辉直播时对五常大米的描述,双11期间,“东方甄选”对五常大米的促销活动是每袋直降5元,会员再享![]() 折优惠,若所推销大米每袋成本为60元,每袋会员价的利润率为
折优惠,若所推销大米每袋成本为60元,每袋会员价的利润率为![]() .
.
(1)求“东方甄选”五常大米的标价;
(2)“东方甄选”为普惠农民,在利润中直接返现9元/袋给农民,若此时“东方甄选”按会员价售卖了10000袋五常大米,共获利多少元?
【答案】(1)“东方甄选”五常大米的标价为89元
(2)共获利多少108000元
【分析】(1)设标价为x元,根据题意找出等量关系,列出方程求解即可;
(2)先求出会员价,再用会员价减去成本和返现,即可求解.
【小问1详解】
解:设“东方甄选”五常大米的标价为x元,
![]() ,
,
解得:![]() .
.
答:“东方甄选”五常大米的标价为89元.
【小问2详解】
由(1)可知,标价为89元,
∴会员价为:![]() (元),
(元),
![]() (元),
(元),
答:共获利多少108000元.
22. 在数轴上,点A,B对应![]() 数分别是
数分别是![]() ,M为线段
,M为线段![]() 的中点,给出如下定义:若
的中点,给出如下定义:若![]() ,则称A是B的“正比点”,例如
,则称A是B的“正比点”,例如![]() 时,A是B的“正比点”.
时,A是B的“正比点”.
(1)若![]() ,则
,则![]() _______,
_______,![]() ________.
________.
下列说法正确的是_______(填序号).
①A是M的“正比点”;②A是B的“正比点”;
③B是M的“正比点”;④B是A的“正比点”.
(2)若![]() ,且M是A、B其中一点的“正比点”,求
,且M是A、B其中一点的“正比点”,求![]() 的值.
的值.
【答案】(1)![]() ,6,③④
,6,③④
(2)![]() 或
或![]()
【分析】(1)根据绝对值和平方的非负性,即可求出a和b的值,再根据“正比点”的定义,即可判断四个说法正确与否;
(2)根据题意,分两种情况进行讨论:当M是A的“正比点”时,当M是B的“正比点”时;即可进行解答.
【小问1详解】
解:∵![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴点M对应的数为:![]() ,
,
令点M对应![]() 数为m,
数为m,
∴![]() ,
,![]() ,
,
∴B是A的“正比点”, B是M的“正比点”,
故答案为:![]() ,6,③④;
,6,③④;
【小问2详解】
点M对应![]() 数为:
数为:![]() ,
,
当M是A的“正比点”时,
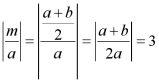 ,
,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ,整理得:
,整理得:![]() 或
或![]() ,
,
∵![]() ,
,
∴![]() ,则
,则![]() ;
;
当M是B的“正比点”时,
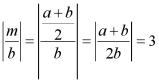 ,
,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ,整理得:
,整理得:![]() 或
或![]() ,
,
∵![]() ,
,
∴![]() ,则
,则![]() ;
;
综上:![]() 或
或![]() .
.