2022-2023学年广东深圳福田区七年级上册期中数学试卷及答案
一、选择题(本题共10小题,每小题3分,共30分,每小题有四个选项,其中只有一个是正确的)
1. ![]() 的倒数是( )
的倒数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 下列各图中,可以是一个正方体的平面展开图的是( )
A. 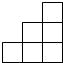 B.
B. 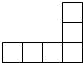 C.
C. 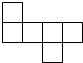 D.
D. 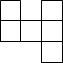
【答案】C
3. 拒绝“餐桌浪费”,刻不容缓.据统计全国每年浪费食物总量约45000000000千克,这个数据用科学记数法表示为()
A. 4.5×1010千克 B. 4.5×109千克 C. 45×109千克 D. 0.45×1011千克
【答案】A
4. 在﹣![]() ,0,﹣|﹣5|,﹣0.6,2,﹣(﹣
,0,﹣|﹣5|,﹣0.6,2,﹣(﹣![]() ),﹣10中负数的个数有( )
),﹣10中负数的个数有( )
A. 3 B. 4 C. 5 D. 6
【答案】B
5. 用一平面去截下列几何体,其截面不可能是长方形的有( )
A. 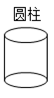 B.
B. 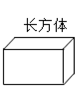 C.
C. 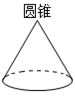 D.
D. 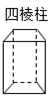
【答案】C
6. 下列代数式符合规范书写要求的是( )
A. ﹣1x B. ![]() C. 0.3÷x D. ﹣
C. 0.3÷x D. ﹣![]() a
a
【答案】D
7. 在数轴上表示3的点与表示![]() 的点之间的距离是( )
的点之间的距离是( )
A. ![]() B. 7 C.
B. 7 C. ![]() D. 4
D. 4
【答案】B
8. 有理数![]() 在数轴上的位置如图所示,则下列各式错误的是()
在数轴上的位置如图所示,则下列各式错误的是()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
9. 华为技术有限公司今年1月份产值a亿元,2月份比1月份减少了10%,则2月份产值达到()
A. ![]() 亿元 B. 10%亿元 C.
亿元 B. 10%亿元 C. ![]() 亿元 D.
亿元 D. ![]() 亿元
亿元
【答案】C
10. 下列说法:
①若一个数的倒数等于它本身,则这个数是1或![]() ;
;
②![]() ,则
,则![]() ;
;
③![]() 是六次三项式;
是六次三项式;
④若a,b互为相反数,则![]() .
.
其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】B
第二部分非选择题
二、填空题(本大题共5小题,每小题3分,共15分)
11. 如果向东走3米记作+3米,那么向西走5米记作______米
【答案】-5
12. 在1,![]() ,0,
,0,![]() 四个数中,最小的数是______.
四个数中,最小的数是______.
【答案】![]()
13. 若![]() +
+![]() =
=![]() ,则
,则![]() 的值是______.
的值是______.
【答案】![]()
14. 如图是正方体的展开图,那么原正方体中,与“党”字所在面对面上的汉字是___________.
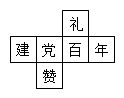
【答案】年
15. 已知a为有理数,如果规定一种新![]() 运算“※”,规定:
运算“※”,规定:![]() ,例如:
,例如:![]() ,计算:
,计算:![]() ___________.
___________.
【答案】![]()
三、解答题(本大题共7小题,其中第16题18分,第17题6分,第18题6分,第19题6分,第20题6分,第21题8分,第22题5分,共55分)
16. 计算:
(1)![]()
(2)![]()
(3)![]()
(4)![]()
(5)![]()
(6)![]()
【答案】(1)8(2)![]()
(3)40(4)10
(5)15(6)39
【分析】(1)先化简符号,再作加减法;
(2)先作乘除法,再作减法;
(3)先化简符号,再除法变乘法,除数变成其倒数,最后约分相乘;
(4)用分配率作乘法,再做加法;
(5)先化简立方,平方,绝对值,再做乘除法,最后作加法;
(6)先作4次方,除法变乘法,除数变成其倒数,化简符号,再作乘法,最后作加法.
【小问1详解】
![]() ;
;
【小问2详解】
![]() ;
;
【小问3详解】
![]() ;
;
【小问4详解】
![]() ;
;
【小问5详解】
![]() ;
;
【小问6详解】
![]() .
.
17. 用数轴上的点表示下列各数:![]() ,-2.5,
,-2.5,![]() ,0,
,0,![]() ,并用“
,并用“![]() ”把它们连接起来.
”把它们连接起来.
![]()
【答案】数轴见解析,![]()
【分析】首先分别在数轴上表示,再根据数轴上的数右边的总比左边的大可得答案.
【详解】解:如图:
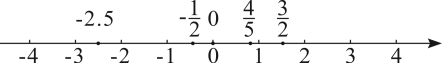
根据数轴可得:![]() .
.
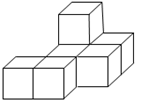
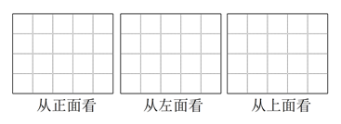
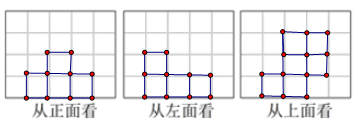
18. 如图是小强用七块相同的小立方体搭成的一个几何体,从正面、左面和上面观察这个几何体,请你在下面相应的位置分别画出你所看到的几何体的形状图.
【答案】见解析.
【分析】根据从正面看到的小正方体个数以及排列方式可得从正面看到的图形,同理可得从左面看到的图形,从上面看到的图形,据此画出即可.
【详解】如图所示:
19. 一只蚂蚁从某点A出发,在一条直线上来回爬行,假定把向右爬行的路程记为正数,向左爬行的路程记为负数,则爬行各段路程(单位:厘米)依次为:
+2,−3,+12,−8,−7,+16,−12,
(1)通过计算说明蚂蚁是否回到起点A;
(2)如果蚂蚁爬行的速度为0.5厘米/秒,那么蚂蚁共爬行了多长时间.
【答案】(1)小虫能回到起点A;(2)小虫共爬行了120秒.
【分析】(1)根据题意列出算式,计算得到结果,即可作出判断;
(2)根据题意列出算式,计算即可得到结果.
【详解】(1)根据题意得:+2−3+12−8−7+16−12=0,
则小虫能回到起点A;
(2)(2+3+12+8+7+16+12)÷0.5=60÷0.5=120(秒),
则小虫共爬行了120秒.
20. 已知a,b互为倒数,![]() 互为相反数,
互为相反数,![]() .根据已知条件请回答:
.根据已知条件请回答:
(1)![]() ___________,
___________,![]() ___________,
___________,![]() ___________
___________![]() ___________;
___________;
(2)求:![]() 的值.
的值.
【答案】(1)1,0,-1,![]()
(2)-1
【分析】(1)根据倒数,相反数,绝对值![]() 意义解答即可;
意义解答即可;
(2)将(1)所得式子的值整体代入计算即可.
【小问1详解】
解:∵a,b互为倒数,
∴![]() ,
,
∵c,d互为相反数,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
故答案为1,0,-1,![]() ;
;
【小问2详解】
解:∵![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() .
.
21. 在数轴上点A表示数a,点B表示数b,点C表示数c,并且a是多项式![]() 的一次项系数,b是最小的正整数,单项式
的一次项系数,b是最小的正整数,单项式![]() 的次数为c.
的次数为c.
(1)![]() ___________,
___________,![]() ___________,
___________,![]() ___________;
___________;
(2)若将数轴在点B处折叠,则点A与点C___________重合(填“能”或“不能”);
(3)若数轴上M、N两点之间的距离为2022(M在N的左侧),且M、N两点在B处折叠后互相重合,则M、N表示的数分别是:M:___________;N:___________.
(4)若在数轴上任意画出一条长是2022个单位的线段,则此线段盖住的整数点的个数是___________.
【答案】(1)![]() ,1,6
,1,6
(2)能(3)![]() ,1012
,1012
(4)2022或2023
【分析】(1)根据多项式、正整数与单项式的概念即可求解;
(2)只需要判断A、C是否关于B对称即可;
(3)由题意可知:M到1与N到1的距离相等,且等于1011,依此即可求解;
(4)由题意可知端点有两种情况,一种是在表示整数的点上,一种是不在表示整数的点上.
【小问1详解】
解:∵多项式![]() 的一次项系数是-4,最小的正整数是1,
的一次项系数是-4,最小的正整数是1,![]() 的次数为6
的次数为6
∴![]()
故答案为:![]() ,1,6
,1,6
【小问2详解】
解:能,理由如下:
由于![]() 与6的中点为
与6的中点为![]() ,故将数轴在点B处折叠,则点A与点C能重合;
,故将数轴在点B处折叠,则点A与点C能重合;
【小问3详解】
解:由题意可知:![]() 的中点是表示1的点,
的中点是表示1的点,
∴M到1与N到1的距离相等,且等于![]() ,
,
∴M表示-1010,1012;
故答案是-1010,1012;
【小问4详解】
解:当端点不在表示整数的点上时,此时整数点共有2022个,
当端点在表示整数的点上时,此时整数点共有![]() 个.
个.
故答案为:2022或2023
22. 阅读材料:求![]() 的值.
的值.
解:设![]()
100将等式两边同时乘以2得
![]()
因此![]()
所以![]()
即![]()
请你仿照此法计算:
(1)![]() ___________;
___________;
(2)求![]() 的值.
的值.
【答案】(1)![]() ##63
##63
(2)![]() .
.
【分析】(1)设![]() ,两边同时乘以2,以材料给出的方法计算即可;
,两边同时乘以2,以材料给出的方法计算即可;
(2)设![]() ,两边同时乘以3,以材料给出的方法计算即可.
,两边同时乘以3,以材料给出的方法计算即可.
【小问1详解】
解:设![]() ①
①
将等式两边同时乘以2,得:![]() ②
②
由![]() 得:
得:![]() ,
,
即![]() 或
或![]() ;
;
【小问2详解】
解:设![]() ①
①
将等式两边同时乘以2,得:![]() ②
②
由![]() 得:
得:![]() ,
,
![]()
![]() ,
,
即![]() ,
,
故![]() .
.