1.B
【分析】根据只有符号不同的两个数互为相反数进行解答即可得.
【详解】解:![]() 的相反数是
的相反数是![]() ,
,
故选:B.
【点睛】本题考查了相反数的定义,熟练掌握相反数的定义是解题的关键.
2.C
【分析】根据三角形的三边关系逐项判断即可得.
【详解】解:A、![]() ,不满足三角形的三边关系,不能搭成三角形,则此项不符合题意;
,不满足三角形的三边关系,不能搭成三角形,则此项不符合题意;
B、![]() ,不满足三角形的三边关系,不能搭成三角形,则此项不符合题意;
,不满足三角形的三边关系,不能搭成三角形,则此项不符合题意;
C、![]() ,满足三角形的三边关系,能搭成三角形,则此项符合题意;
,满足三角形的三边关系,能搭成三角形,则此项符合题意;
D、![]() ,不满足三角形的三边关系,不能搭成三角形,则此项不符合题意;
,不满足三角形的三边关系,不能搭成三角形,则此项不符合题意;
故选:C.
【点睛】本题考查了三角形的三边关系,解题的关键是熟练掌握三角形的三边关系:任意两边之和大于第三边、任意两边之差小于第三边.
3.B
【分析】根据合并同类项法则、同底数幂的乘法、积的乘方与幂的乘方法则逐项判断即可得.
【详解】解:A、![]() ,则此项错误,不符合题意;
,则此项错误,不符合题意;
B、![]() ,则此项正确,符合题意;
,则此项正确,符合题意;
C、![]() ,则此项错误,不符合题意;
,则此项错误,不符合题意;
D、![]() ,则此项错误,不符合题意;
,则此项错误,不符合题意;
故选:B.
【点睛】本题考查了合并同类项、同底数幂的乘法、积的乘方与幂的乘方,熟练掌握各运算法则是解题关键.
4.C
【分析】根据中位数的定义(将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数)即可得.
【详解】解:将这组数据按从小到大进行排序为89,92,95,96,98,
则其中位数是95,
故选:C.
【点睛】本题考查了中位数,熟记中位数的概念是解题关键.
5.C
【分析】先判断出![]() 的内角是这个等腰三角形的顶角,再根据等腰三角形的定义求解即可得.
的内角是这个等腰三角形的顶角,再根据等腰三角形的定义求解即可得.
【详解】解:![]() 等腰三角形有一个内角为
等腰三角形有一个内角为![]() ,
,
∴这个等腰三角形的底角是![]() ,
,
故选:C.
【点睛】本题考查了等腰三角形的定义,三角形内角和定理,解题的关键是熟练掌握等腰三角形的两个底角相等.
6.D
【分析】根据每三人乘一车,最终剩余2辆车,每2人乘一车,最终剩余9人无车可乘,进而表示出总人数得出等式即可;
【详解】由题意可列出方程![]() ,
,
故选D.
【点睛】本题主要考查了一元一次方程的应用,准确分析列方程是解题的关键.
7.B
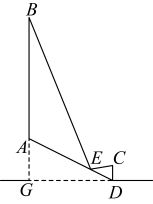
【分析】过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,判断出当点
,判断出当点![]() 为
为![]() 的延长线与
的延长线与![]() 的交点时,点
的交点时,点![]() 到直线
到直线![]() 的距离最大,由此即可得.
的距离最大,由此即可得.
【详解】解:如图,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,

![]() ,
,![]() ,
,
![]() 当点
当点![]() 为
为![]() 的延长线与
的延长线与![]() 的交点时,点
的交点时,点![]() 到直线
到直线![]() 的距离最大,最大距离为
的距离最大,最大距离为![]() ,
,
故选:B.
【点睛】本题考查了圆的性质,正确判断出点![]() 到直线
到直线![]() 的距离最大时,点
的距离最大时,点![]() 的位置是解题关键.
的位置是解题关键.
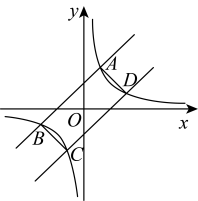
8.A
【分析】连接四边形![]() 的对角线
的对角线![]() ,过
,过![]() 作
作![]() 轴,过
轴,过![]() 作
作![]() 轴,直线
轴,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,如图所示,根据函数图像交点的对称性判断四边形
,如图所示,根据函数图像交点的对称性判断四边形![]() 是平行四边形,由平行四边形性质及平面直角坐标系中三角形面积求法,确定
是平行四边形,由平行四边形性质及平面直角坐标系中三角形面积求法,确定![]() ,再求出直线
,再求出直线![]() 与
与![]() 轴交于点
轴交于点![]() ,通过联立
,通过联立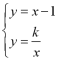 求出
求出![]() 纵坐标,代入方程求解即可得到答案.
纵坐标,代入方程求解即可得到答案.
【详解】解:连接四边形![]() 的对角线
的对角线![]() ,过
,过![]() 作
作![]() 轴,过
轴,过![]() 作
作![]() 轴,直线
轴,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,如图所示:
,如图所示:

根据直线![]() 、
、![]() 与双曲线
与双曲线![]() 交点的对称性可得四边形
交点的对称性可得四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() 直线
直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ,
,
![]()
![]() 与双曲线
与双曲线![]() 分别相交于点
分别相交于点![]() ,
,
![]() 联立
联立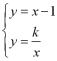 ,即
,即![]() ,则
,则![]() ,由
,由![]() ,解得
,解得![]() ,
,
![]()
![]() ,即
,即![]() ,解得
,解得![]() ,
,
故选:A.
【点睛】本题考查一次函数与反比例函数综合,涉及平行四边形的判定与性质,熟练掌握平面直角坐标系中三角形面积求法是解决问题的关键.
9.![]()
【分析】根据算术平方根进行计算即可求解.
【详解】解:![]()
![]() ,
,
故答案为:![]() .
.
【点睛】本题考查了求一个数的算术平方根,熟练掌握算术平方根的定义是解题的关键.
10.![]()
【分析】用科学记数法表示较大的数时,一般形式为![]() ,其中
,其中![]() ,
,![]() 为整数,按要求表示即可.
为整数,按要求表示即可.
【详解】解:55000共有5位数,从而用科学记数法表示为![]() ,
,
故答案为:![]() .
.
【点睛】本题考查科学记数法,按照定义,确定![]() 与
与![]() 的值是解决问题的关键.
的值是解决问题的关键.
11.![]()
【分析】直接提取公因式![]() 即可
即可
【详解】解:![]() .
.
故答案为: ![]() .
.
12.3
【分析】根据一元一次不等式的解法即可得.
【详解】解:不等式![]() 的解集是
的解集是![]() ,
,
则不等式![]() 的最大整数解是3,
的最大整数解是3,
故答案为:3.
【点睛】本题考查了解一元一次不等式,熟练掌握一元一次不等式的解法是解题关键.
13.![]()
【分析】由n边形的内角和是:180°(n-2),将n=7代入即可求得答案.
【详解】解:七边形的内角和是:180°×(7-2)=900°.
故答案为:900°.
【点睛】此题考查了多边形的内角和,熟记n边形的内角和公式是解题的关键.
14.![]()
【分析】根据关于x轴的对称点的坐标计算即可;
【详解】根据关于x轴的对称点的特征,横坐标不变,纵坐标变为相反数可得:点![]() 关于
关于![]() 轴对称的点的坐标是
轴对称的点的坐标是![]() ;
;
故答案是![]() .
.
【点睛】本题主要考查了平面直角坐标系中点的对称,准确计算是解题的关键.
15.6
【分析】先根据圆锥的底面半径求出底面圆周长,也就是侧面图扇形的弧长,再利用弧长公式求出扇形半径,也就是圆锥的母线.
【详解】解:∵圆锥的底面半径是2,
∴底面圆周长是![]() ,即展开后的扇形弧长是
,即展开后的扇形弧长是![]() ,
,
根据弧长公式:![]() ,
,
得![]() ,解得
,解得![]() ,即该圆锥的母线长是6.
,即该圆锥的母线长是6.
故答案是:6.
【点睛】本题考查扇形和圆锥的有关计算,解题的关键是掌握扇形的弧长公式,以及圆锥和侧面展开的扇形的关系.
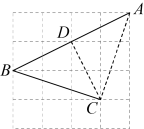
16.![]()
【分析】取![]() 的中点
的中点![]() ,连接
,连接![]() ,先根据勾股定理可得
,先根据勾股定理可得![]() ,再根据等腰三角形的三线合一可得
,再根据等腰三角形的三线合一可得![]() ,然后根据正弦的定义即可得.
,然后根据正弦的定义即可得.
【详解】解:如图,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
![]() ,
,
![]() ,
,
又![]() 点
点![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() ,
,
故答案为:![]() .
.
【点睛】本题考查了勾股定理与网格问题、等腰三角形的三线合一、正弦,熟练掌握正弦的求解方法是解题关键.
17.![]()
【分析】根据完全平方公式得![]() ,再代值计算即可.
,再代值计算即可.
【详解】解:![]()
![]()
![]()
![]()
![]()
![]()
故答案为:![]() .
.
【点睛】本题考查完全平方公式的应用,求代数式值,掌握完全平方公式![]() 及其变式是解题本题的关键.
及其变式是解题本题的关键.
18.![]()
【分析】首先画出图形,然后得到旋转3次为一循环,然后求出点![]() 在射线
在射线![]() 的延长线上,点
的延长线上,点![]() 在x轴的正半轴上,然后利用旋转的性质得到
在x轴的正半轴上,然后利用旋转的性质得到![]() ,最后利用勾股定理和含
,最后利用勾股定理和含![]() 角直角三角形的性质求解即可.
角直角三角形的性质求解即可.
【详解】如图所示,
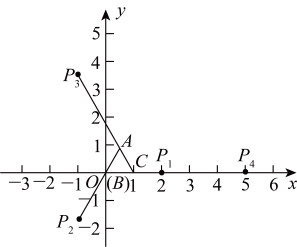
由图象可得,点![]() ,
,![]() 在x轴的正半轴上,
在x轴的正半轴上,
∴.旋转3次为一个循环,
∵![]()
∴点![]() 在射线
在射线![]() 的延长线上,
的延长线上,
∴点![]() 在x轴的正半轴上,
在x轴的正半轴上,
∵![]() ,
,![]() 是正三角形,
是正三角形,
∴由旋转的性质可得,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴同理可得,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴由旋转的性质可得,![]() ,
,
∴如图所示,过点![]() 作
作![]() 轴于点E,
轴于点E,
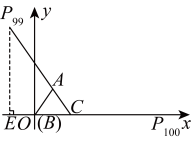
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴点![]() 的坐标是
的坐标是![]() .
.
故答案为:![]() .
.
【点睛】本题考查了坐标与图形变化-旋转,勾股定理,等边三角形的性质.正确确定每次旋转后点与旋转中心的距离长度是关键.
19.![]()
【分析】根据去绝对值运算、零指数幂运算及特殊角的三角函数值分别计算后,再根据二次根式加减运算法则求解即可得到答案.
【详解】解:![]()
![]()
![]() .
.
【点睛】本题考查二次根式加减运算,涉及去绝对值运算、零指数幂运算及特殊角的三角函数值,熟练掌握相关运算法则是解决问题的关键.
20.![]() ,原式
,原式![]()
【分析】先根据分式的混合计算法则化简,然后代值计算即可.
【详解】解:![]()
![]()
![]()
![]() ,
,
当![]() 时,原式
时,原式![]() .
.
【点睛】本题主要考查了分式的化简求值,正确计算是解题的关键.
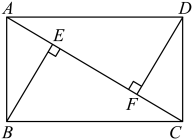
21.证明见解析
【分析】根据![]() 定理证出
定理证出![]() ,再根据全等三角形的性质即可得证.
,再根据全等三角形的性质即可得证.
【详解】证明:![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,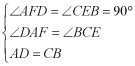 ,
,
![]() ,
,
![]() .
.
【点睛】本题考查了矩形的性质、三角形全等的判定与性质等知识点,熟练掌握矩形的性质是解题关键.
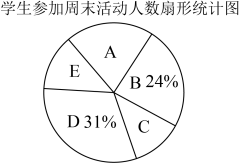
22.(1)24,62
(2)72
(3)估算该校九年级周末参加家务劳动的人数为96名
【分析】(1)先根据![]() 的扇形统计图和统计表信息可求出抽取调查的学生总人数,再根据
的扇形统计图和统计表信息可求出抽取调查的学生总人数,再根据![]() 的扇形统计图可求出
的扇形统计图可求出![]() 的值,然后利用抽取调查的学生总人数减去其他活动的人数可得
的值,然后利用抽取调查的学生总人数减去其他活动的人数可得![]() 的值;
的值;
(2)利用![]() 乘以
乘以![]() 的学生人数所占百分比即可得;
的学生人数所占百分比即可得;
(3)利用该校九年级的学生总人数乘以周末参加家务劳动的学生人数所占百分比即可得.
【详解】(1)解:抽取调查的学生总人数为![]() (人),
(人),
则![]() (人),
(人),
![]() (人),
(人),
故答案为:24,62.
(2)解:![]() ,
,
即扇形统计图中![]() 对应的圆心角是72度,
对应的圆心角是72度,
故答案为:72.
(3)解:![]() (名),
(名),
答:估算该校九年级周末参加家务劳动的人数为96名.
【点睛】本题考查了统计表和扇形统计图、利用样本估计总体等知识点,熟练掌握统计调查的相关知识是解题关键.
23.(1)![]()
(2)![]()
【分析】(1)直接利用概率公式求解;
(2)画树状图展示所有等可能的结果数,找出选中1名男生和1名女生的结果数,然后根据概率公式求解.
【详解】(1)解:只选1名选手参加比赛,女生D入选的概率![]()
故答案为:![]() ;
;
(2)画树状图为如下:
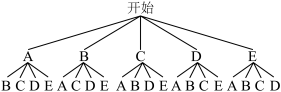
共有20种等可能的结果数,其中选中1名男生和1名女生的有12种![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以恰好选中1名男生和1名女生的概率![]() .
.
【点睛】本题考查了利用概率公式求概率,列表法与树状图法,利用列表法或树状图法展示所有可能的结果数,再从中选出符合事件的结果数,然后根据概率公式计算事件的概率.
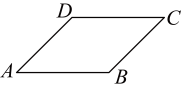
24.(1)![]()
(2)作图见解析
【分析】(1)连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,如图所示,由勾股定理先求出
,如图所示,由勾股定理先求出![]() ,在
,在![]() 中再由勾股定理,
中再由勾股定理,![]() ;
;
(2)连接![]() ,根据轴对称性质,过点
,根据轴对称性质,过点![]() 尺规作图作线段
尺规作图作线段![]() 的垂直平分线即可得到答案.
的垂直平分线即可得到答案.
【详解】(1)解:连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,如图所示:
,如图所示:
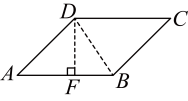
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
(2)解:如图所示:

【点睛】本题考查平行四边形背景下求线段长,涉及勾股定理、尺规作图作线段垂直平分线,熟练掌握勾股定理求线段长及中垂线的尺规作图是解决问题的关键.
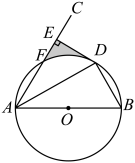
25.(1)②①,证明见解析(或①②,证明见解析)(2)![]()
【分析】(1)一:已知条件为②![]() ,结论为①
,结论为①![]() 与
与![]() 相切;连接
相切;连接![]() ,先证出
,先证出![]() ,再根据平行线的性质可得
,再根据平行线的性质可得![]() ,然后根据圆的切线的判定即可得证;二:已知条件为①
,然后根据圆的切线的判定即可得证;二:已知条件为①![]() 与
与![]() 相切,结论为②
相切,结论为②![]() ;连接
;连接![]() ,先证出
,先证出![]() ,再根据圆的切线的性质可得
,再根据圆的切线的性质可得![]() ,然后根据平行线的性质即可得证;
,然后根据平行线的性质即可得证;
(2)连接![]() ,先解直角三角形求出
,先解直角三角形求出![]() 的长,再根据等边三角形的判定与性质可得
的长,再根据等边三角形的判定与性质可得![]() 的长,从而可得
的长,从而可得![]() 的长,然后根据圆周角定理可得
的长,然后根据圆周角定理可得![]() ,最后根据阴影部分的面积等于直角梯形
,最后根据阴影部分的面积等于直角梯形![]() 的面积减去扇形
的面积减去扇形![]() 的面积即可得.
的面积即可得.
【详解】解:(1)一:已知条件为②![]() ,结论为①
,结论为①![]() 与
与![]() 相切,证明如下:
相切,证明如下:
如图,连接![]() ,
,
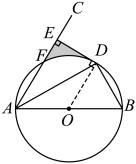
![]() ,
,
![]() ,
,
![]() 弦
弦![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() 是
是![]() 的半径,
的半径,
![]() 与
与![]() 相切;
相切;
二:已知条件为①![]() 与
与![]() 相切,结论为②
相切,结论为②![]() ,证明如下:
,证明如下:
如图,连接![]() ,
,

![]() ,
,
![]() ,
,
![]() 弦
弦![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 与
与![]() 相切,
相切,
![]() ,
,
![]() ;
;
(2)如图,连接![]() ,
,
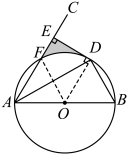
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
由圆周角定理得:![]() ,
,
则阴影部分的面积为![]()
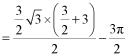
![]() .
.
【点睛】本题考查了圆的切线的判定与性质、解直角三角形、扇形的面积、圆周角定理等知识点,熟练掌握圆的切线的判定与性质是解题关键.
26.(1)![]() 的销售单价为
的销售单价为![]() 元、
元、![]() 的销售单价为
的销售单价为![]() 元
元
(2)当![]() 时,商场销售
时,商场销售![]() 两种商品可获得总利润最大,最大利润是
两种商品可获得总利润最大,最大利润是![]() 元.
元.
【分析】(1)设![]() 的销售单价为
的销售单价为![]() 元、
元、![]() 的销售单价为
的销售单价为![]() 元,根据题中售出
元,根据题中售出![]() 种20件,
种20件,![]() 种10件,销售总额为840元;售出
种10件,销售总额为840元;售出![]() 种10件,
种10件,![]() 种15件,销售总额为660元列方程组求解即可得到答案;
种15件,销售总额为660元列方程组求解即可得到答案;
(2)设利润为![]() ,根据题意,得到
,根据题意,得到![]() ,结合二次函数性质及题中限制条件分析求解即可得到答案.
,结合二次函数性质及题中限制条件分析求解即可得到答案.
【详解】(1)解:设![]() 的销售单价为
的销售单价为![]() 元、
元、![]() 的销售单价为
的销售单价为![]() 元,则
元,则
![]() ,解得
,解得![]() ,
,
答:![]() 的销售单价为
的销售单价为![]() 元、
元、![]() 的销售单价为
的销售单价为![]() 元;
元;
(2)解:![]()
![]() 种商品售价不低于
种商品售价不低于![]() 种商品售价,
种商品售价,
![]() ,解得
,解得![]() ,即
,即![]() ,
,
设利润为![]() ,则
,则
![]()
![]()
![]() ,
,
![]() ,
,
![]() 在
在![]() 时能取到最大值,最大值为
时能取到最大值,最大值为![]() ,
,
![]() 当
当![]() 时,商场销售
时,商场销售![]() 两种商品可获得总利润最大,最大利润是
两种商品可获得总利润最大,最大利润是![]() 元.
元.
【点睛】本题考查二元一次方程组及二次函数解实际应用题,读懂题意,根据等量关系列出方程组,根据函数关系找到函数关系式分析是解决问题的关键.
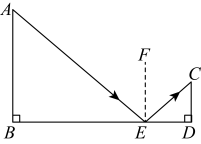
27.[问题背景] ![]() ;[活动探究]
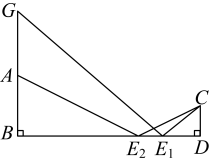
;[活动探究] ![]() ;[应用拓展]
;[应用拓展] ![]()
【分析】[问题背景]根据反射定理,结合两个三角形相似的判定与性质,列出相似比代值求解即可得到答案;
[活动探究] 根据反射定理,结合两个三角形相似的判定与性质,运用两次三角形相似,列出相似比代值,作差求解即可得到答案;
[应用拓展] 延长![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,如图所示,由坡比可求出相关线段长,再根据反射定理,结合两个三角形相似的判定与性质,列出相似比代值求解,最后由勾股定理求出
,如图所示,由坡比可求出相关线段长,再根据反射定理,结合两个三角形相似的判定与性质,列出相似比代值求解,最后由勾股定理求出![]() 长即可得到答案.
长即可得到答案.
【详解】解:[问题背景]如图所示:
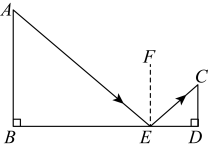
![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,
![]() ,解得
,解得![]() ;
;
[活动探究]如图所示:

![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,解得
,解得![]() ;
;
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,解得
,解得![]() ;
;
![]() ;
;
[应用拓展]延长![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,如图所示:
,如图所示:
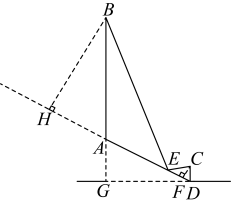
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 坡比为
坡比为![]() (即
(即![]() ),
),![]() ,设
,设![]() ,
,
![]()
![]() ,解得
,解得![]() ,
,
![]() ,
,
![]() ,
,![]() ,设
,设![]() ,
,
![]()
![]() ,解得
,解得![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() .
.
【点睛】本题考查解直角三角形综合,涉及相似三角形的判定与性质、三角函数求线段长、勾股定理等知识,读懂题意,熟练掌握相似三角形测高、三角函数测高的方法步骤是解决问题的关键.
28.(1)②
(2)![]() ;
;![]() 、
、![]()
(3)![]()
【分析】(1)在平面直角坐标系中作出![]() ;
;![]() ;
;![]() ;
;![]() 图像,结合“兄弟函数”定义即可得到答案;
图像,结合“兄弟函数”定义即可得到答案;
(2)①根据“兄弟函数”定义,当![]() 时,求出
时,求出![]() 值,列方程求解即可得到答案;②联立方程组求解即可得到答案;
值,列方程求解即可得到答案;②联立方程组求解即可得到答案;
(3)根据“兄弟函数”定义,联立方程组,分类讨论,由![]() ,按照讨论结果求解,即可得到答案.
,按照讨论结果求解,即可得到答案.
【详解】(1)解:作出![]() ;
;![]() ;
;![]() ;
;![]() 图像,如图所示:
图像,如图所示:
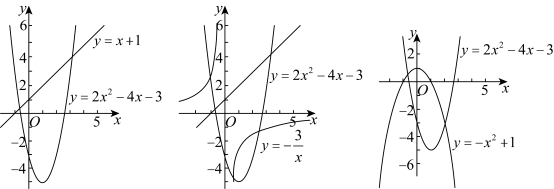
![]()
![]() 与
与![]() 图像有三个不同的公共点,
图像有三个不同的公共点,
根据“兄弟函数”定义,与二次函数![]() 互为“兄弟函数”的是②,
互为“兄弟函数”的是②,
故答案为:②;
(2)解:①![]() 函数
函数![]() 与
与![]() 互为“兄弟函数”,
互为“兄弟函数”,![]() 是其中一个“兄弟点”的横坐标,
是其中一个“兄弟点”的横坐标,
![]() ,则
,则![]() ,解得
,解得![]() ;
;
②联立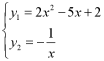 ,即
,即![]() ,
,
![]() 是其中一个解,
是其中一个解,
![]() 因式分解得
因式分解得![]() ,则
,则![]() ,解得
,解得![]() ,
,
![]() 另外两个“兄弟点”的横坐标是
另外两个“兄弟点”的横坐标是![]() 、
、![]() ;
;
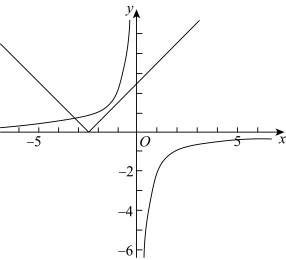
(3)解:在平面直角坐标系中作出![]() (m为常数)与
(m为常数)与![]() 图像,如图所示:
图像,如图所示:
联立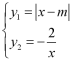 ,即
,即![]() ,
,
①当![]() 时,
时,![]() ,即
,即![]() ,当
,当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ,即
,即![]() ,由①中
,由①中![]() ,则
,则![]() ,
,![]() ;
;
由图可知,两个函数的交点只能在第二象限,从而![]() ,再根据三个“兄弟点”的横坐标分别为
,再根据三个“兄弟点”的横坐标分别为![]() 、
、![]() 、
、![]() ,且
,且![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]()
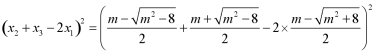
![]()
![]()
![]() ,
,
由![]() 得到
得到![]() ,即
,即![]() .
.
【点睛】本题考查函数综合,涉及新定义函数,搞懂题意,按照“兄弟函数”、“兄弟点”定义数形结合是解决问题的关键.