![]()
2023-2024学年浙江省金华市义乌市八年级上学期10月月考数学试题及答案
一、选择愿(本大题共10小题,每小题3分,共30分)
1.下列运动图标中,属于轴对称图形的是( )
A. B.
B.
C. D.
D.
2.现有两根长度分别这![]() 和
和![]() 的木棒,若要钉成一个三角形木棒,则第三根木棒长可以为( )
的木棒,若要钉成一个三角形木棒,则第三根木棒长可以为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下列选项中,可以用来说明命题“若![]() ,则
,则![]() ”是假命题的反例是( )
”是假命题的反例是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.如图用直尺和圆规作已知角的平分线的示意图,由![]() 可得
可得![]() ,由作图的过程可知,说明
,由作图的过程可知,说明![]() 的依据是( )
的依据是( )
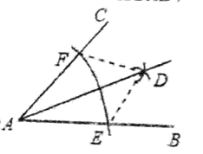
A.SSS B.SAS C.ASA D.AAS
5.等腰三角形两边长分别为2和4,则这个等腰三角形的周长为( )
A.6 B.8 C.10 D.8或10
6.如图,已知![]() ,用尺规在:
,用尺规在:![]() 上确定一点
上确定一点![]() ,仗
,仗![]() ,则下列选项中,一定得合要求的作图痕迹是( )
,则下列选项中,一定得合要求的作图痕迹是( )
A.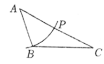 B.
B.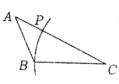
C.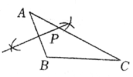 D.
D.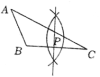
7.如图,在![]() 中,
中,![]() 于点
于点![]() 于点
于点![]() 于点
于点![]() ,则
,则![]() ( )
( )
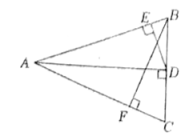
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.如图,在![]() 中,
中,![]() 边上的高为
边上的高为![]() ,在
,在![]() 中,
中,![]() 边上的高为
边上的高为![]() .下列结论中,正确的是( )
.下列结论中,正确的是( )
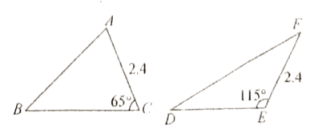
A.![]() B.
B.![]() C.
C.![]() D.无法确定
D.无法确定
9.如图,![]() 与
与![]() 中,
中,![]() 交
交![]() 于
于![]() .给出下列结论:①
.给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )个.
.其中正确的结论有( )个.
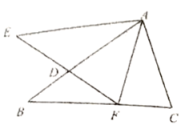
A.1 B.2 C.3 D.4
10.如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的平分线.若
的平分线.若![]() 分别是
分别是![]() 和
和![]() 上的动点,则
上的动点,则![]() 的最小值是( )
的最小值是( )
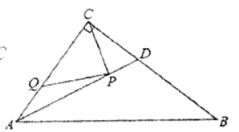
A.2.4 B.4.8 C.4 D.5
二、填空题(本大题共6小题,每小题4分,共24分)
11.如图,![]() ,若要证明
,若要证明![]() ,需要补充的一个条件是___________.(写出一个即可)
,需要补充的一个条件是___________.(写出一个即可)
12.如图,若![]() ,则
,则![]() 的大小为___________.
的大小为___________.
13.如图,![]() 中,
中,![]() 是
是![]() 边上的一点(不与
边上的一点(不与![]() 重合),点
重合),点![]() 是线段
是线段![]() 的三等分点,记
的三等分点,记![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,若
,若![]() ,则
,则![]() 的面积为___________.
的面积为___________.
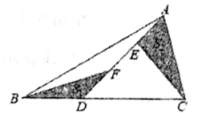
14.如图,在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 的中点,连结
的中点,连结![]() ,若
,若![]() ,则
,则![]() 的面积为___________.
的面积为___________.
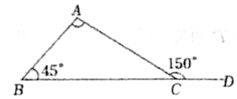
15.等腰三角形一腰上的高与另一腰的夹角是![]() ,则这个等腰三角形的顶角为___________.
,则这个等腰三角形的顶角为___________.
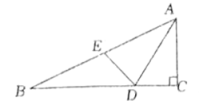
16.如图,![]() 平分
平分![]() 于点
于点![]() ,那么
,那么![]() 的长度为___________
的长度为___________![]() .
.
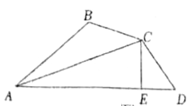
三、解答题(本大题共8小题,第17~19题每题6分,第20~21题每题8分,第22~23题每题10分,第24题12分,共66分,解答题需写出必要的文字说明,演算步骤或证明过程)
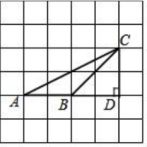
17.如图,在![]() 的正方形网格中,每个小正方形的边长都为1.
的正方形网格中,每个小正方形的边长都为1.
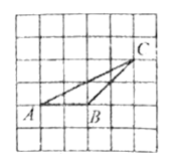
(1)利用网格,作![]() 的高线
的高线![]() .
.
(2)![]() 的面积为___________.
的面积为___________.
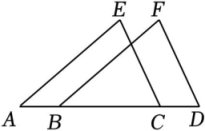
18.如图,点![]() 在同一直线上,
在同一直线上,![]() .求证:
.求证:![]() .
.
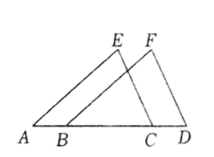
19.如图,在![]() 中,
中,![]() 为
为![]() 延长线上一点,
延长线上一点,![]() ,交
,交![]() 于点
于点![]() .求证:
.求证:![]() .
.
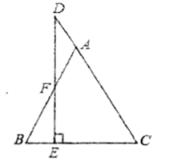
20.如图,点![]() 在
在![]() 的边
的边![]() 上,
上,![]() ,求证:
,求证:![]() .
.

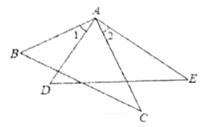
21.如图,已知![]() 分别是
分别是![]() 的边
的边![]() 上的点,且
上的点,且![]() .
.
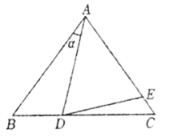
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)设![]() ,请你判断
,请你判断![]() 是否存在数量关系,写出你的结论并证明.
是否存在数量关系,写出你的结论并证明.
22.如图1,已知线段![]() 相交于点
相交于点![]() ,连接
,连接![]() ,则我们把形如这样的图形称为“8字型”.
,则我们把形如这样的图形称为“8字型”.
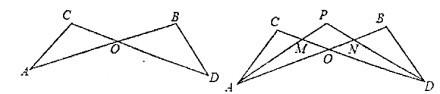
图1 图2
(1)求证:![]() ;
;
(2)如图2,若![]() 和
和![]() 的平分线
的平分线![]() 和
和![]() 相交于点
相交于点![]() ,且与
,且与![]() 分別相交于点
分別相交于点![]() .
.
①以线段![]() 为边的“8字型”有___________个,以点
为边的“8字型”有___________个,以点![]() 为交点的“8字型”有___________个;
为交点的“8字型”有___________个;
②若![]() ,求
,求![]() 的度数;
的度数;
③若角平分线中角的关系改为“![]() ”,试探究
”,试探究![]() 与
与![]() 之间存在的数量关系,并说明理由.
之间存在的数量关系,并说明理由.
23.通过对数学模型“K字”模型或“一线三等角”模型的研究学习,解决下列问题:
【模型坐现】如图1,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .求证:
.求证:![]() .
.
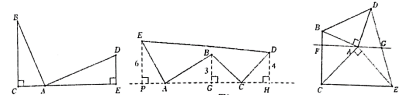
图1图2图3
【模型应用】如图2,![]() 且
且![]() 且
且![]() ,请按照图中所标注的数据,计算图中实线所围成的图形的面积.
,请按照图中所标注的数据,计算图中实线所围成的图形的面积.
【深入探究】如图3,![]() ,连接
,连接![]() ,且.
,且.![]() 于点
于点![]() 与直线
与直线![]() 交于点
交于点![]() .若
.若![]() ,则
,则![]() 的面积为___________.(直接写出结果)
的面积为___________.(直接写出结果)
24.如图①,在![]() 中,
中,![]() ,现有一动点
,现有一动点![]() ,从点
,从点![]() 出发,沿着三角形的边
出发,沿着三角形的边![]() 运动,回到点
运动,回到点![]() 停止,速度为
停止,速度为![]() ,
,
设运动时间为![]() 秒.
秒.
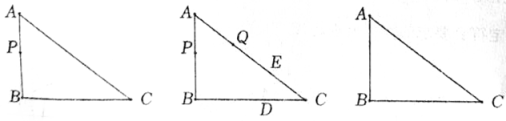
图① 图② 备用图
(1)如图①,当![]() 的面积等于
的面积等于![]() 面积的一半时,求
面积的一半时,求![]() 的值:
的值:
(2)如图②,点![]() 在
在![]() 边上
边上![]() ,点
,点![]() 在
在![]() 边上
边上![]() ,在
,在![]() 的边上,若另外有一个动点
的边上,若另外有一个动点![]() 与点
与点![]() 同时从点
同时从点![]() 出发,沿着边
出发,沿着边![]() 运动,回到点
运动,回到点![]() 停止.在两点运动过程中的某一时刻,以
停止.在两点运动过程中的某一时刻,以![]() 为顶点的三角形恰好与
为顶点的三角形恰好与![]() 全等,求点
全等,求点![]() 的运动速度.
的运动速度.
参考答案
一、选择题
BCDACCBCCB
二、填空题
11.略 12.![]() 13.12 14.36 15.
13.12 14.36 15.![]() 或
或![]() 16.3.5
16.3.5
三、解答题
17.(1)如图所示:![]() 即为所求;
即为所求;
(2)2.
18.证明:![]() ,
,
![]() ,
,
即![]() ,
,
在![]() 和
和![]() 中,
中,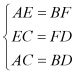 ,
,
![]() .
.
19.证明:在![]() 中,
中,
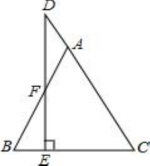
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() .
.
20.证明:作![]() 于点
于点![]() ,
,
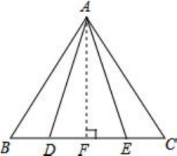
![]()
![]()
![]()
![]()
![]()
即![]()
21.解:(1)![]() ,
,
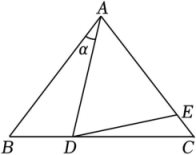
![]() ,
,
又![]() ,
,
![]() ,
,
即![]() ,
,
![]() ,
,
![]() ;
;
(2)![]() ,理由如下:
,理由如下:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
即![]() ,
,
![]() .
.
22.(1)证明:在图1中,有![]() ,
,
![]() ,
,
![]() ;
;
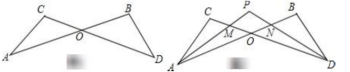
图1图2
(2)解:①3;4;
②以![]() 为交点“8字型”中,有
为交点“8字型”中,有![]() ,
,
以![]() 为交点“8字型”中,有
为交点“8字型”中,有![]()
![]() ,
,
![]() 分别平分
分别平分![]() 和
和![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
③![]() ,其理由是:
,其理由是:
![]() ,
,
![]() ,
,
以![]() 为交点“8字型”中,有
为交点“8字型”中,有![]() ,
,
以![]() 为交点“8字型”中,有
为交点“8字型”中,有![]()
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
23.【模型呈现】证明:![]() ,
,
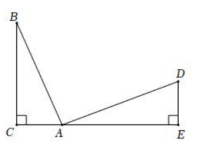
图1
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,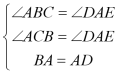 ,
,
![]() ,
,
![]() ;
;
【模型应用】解:由【模型呈现】可知,![]() ,
,
![]() ,
,
则![]() ,故答案为:50;
,故答案为:50;

图2
【深入探究】过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,
,
由【模型呈现】可知,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
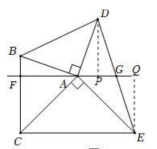
图3
24.(1)![]() 或19
或19