![]()
2023-2024学年天津市西青区九年级上学期数学月考试卷及答案
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列方程是关于x的一元二次方程的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】
【分析】根据只含有一个未知数,并且未知数的最高次数是2的整式方程叫一元二次方程进行分析即可.
【详解】解:A.![]() 中未知数的指数不是2,故不是一元二次方程,不符合题意;
中未知数的指数不是2,故不是一元二次方程,不符合题意;
B.![]() 中含有2个未知数,故不是一元二次方程,不符合题意;
中含有2个未知数,故不是一元二次方程,不符合题意;
C.![]() ,该方程是分式方程,故本选项不合题意;
,该方程是分式方程,故本选项不合题意;
D、![]() ,该方程是一元二次方程,故本选项符合题意;
,该方程是一元二次方程,故本选项符合题意;
故选:D.
【点睛】此题主要考查了一元二次方程的定义,解题的关键是掌握判断一个方程是否是一元二次方程应注意抓住5个方面:“化简后”;“一个未知数”;“未知数的最高次数是2”;“二次项的系数不等于0”;“整式方程”.
2. 方程![]() 的根的情况是( )
的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根 C. 无实数根 D. 只有一个实数根
【答案】C
【解析】
【分析】把a=1,b=-1,c=3代入△=b2-4ac进行计算,然后根据计算结果判断方程根的情况.
【详解】∵a=1,b=-1,c=3,
∴△=b2-4ac=(-1)2-4×1×3=-11<0,
所以方程没有实数根.
故选C.
【点睛】本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.
3. 抛物线![]() 的顶点坐标是( )
的顶点坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
【分析】根据抛物线的顶点式![]() 的顶点坐标为
的顶点坐标为![]() ,即可得出结论.
,即可得出结论.
【详解】解:抛物线![]() 的顶点坐标是
的顶点坐标是![]() .
.
故选:A.
【点睛】本题主要考查了二次函数的图像与性质,掌握二次函数的顶点式的特征是解题的关键.
4. 一元二次方程3x2﹣2=4x可化成一般形式为( )
A. 3x2﹣4x+2=0 B. 3x2﹣4x﹣2=0 C. 3x2+4x+2=0 D. 3x2+4x﹣2=0
【答案】B
【解析】
【分析】将方程整理为一般形式即可.
【详解】解:方程整理得:3x2﹣4x﹣2=0.
故选:B.
【点睛】此题考查了一元二次方程的一般形式,其一般形式为ax2+bx+c=0(a,b,c为常数且a≠0).
5. 二次函数![]() 的图象大致是( )
的图象大致是( )
A. 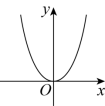 B.
B. 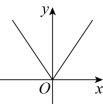
C. 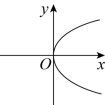 D.
D. 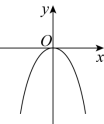
【答案】A
【解析】
【分析】根据二次函数的图像和性质,逐一判断图像即可.
【详解】解:![]() 的图像是一条过原点,开口向上的抛物线,
的图像是一条过原点,开口向上的抛物线,
故选A.
【点睛】本题主要考查二次函数的图像和性质,熟练掌握二次函数的图像与二次函数的系数的关系是解题的关键.
6. 抛物线![]() 的顶点坐标为(0,1),则抛物线的解析式为( )
的顶点坐标为(0,1),则抛物线的解析式为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
【分析】把顶点坐标代入解析式中求出c的值即可.
【详解】∵抛物线![]() 的顶点坐标为(0,1),
的顶点坐标为(0,1),
∴c=1,
∴抛物线的解析式为:![]() .
.
故选A.
【点睛】本题考查了待定系数法求二次函数解析式,待定系数法是求函数解析式常用的方法,需熟练掌握并灵活运用.
7. 在某篮球邀请赛中,参赛的每两个队之间都要比赛一场,共比赛36场,设有x个队参赛,根据题意,可列方程为()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
【分析】共有x个队参加比赛,则每队参加(x-1)场比赛,但2队之间只有1场比赛,根据共安排36场比赛,列方程即可.
【详解】解:设有x个队参赛,根据题意,可列方程为:
![]() x(x﹣1)=36,
x(x﹣1)=36,
故选A.
【点睛】此题考查由实际问题抽象出一元二次方程,解题关键在于得到比赛总场数的等量关系.
8. 抛物线![]() 不经过的象限是( )
不经过的象限是( )
A. 第一、二象限 B. 第二、四象限
C. 第三、四象限 D. 第二、三象限
【答案】A
【解析】
【分析】根据![]() ,可得抛物线
,可得抛物线![]() 的图象在x轴下方,问题得解.
的图象在x轴下方,问题得解.
【详解】解:∵![]() ,
,
∴抛物线![]() 的图象在x轴下方,
的图象在x轴下方,
∴抛物线![]() 不经过的象限是第一、二象限,
不经过的象限是第一、二象限,
故选:A.
【点睛】本题主要考查了二次函数的图象与性质,根据![]() ,得出抛物线
,得出抛物线![]() 的图象在x轴下方,是解答本题的关键.
的图象在x轴下方,是解答本题的关键.
9. 下列一元二次方程没有实数根的是( )
A. x2+x+1=0 B. x2+x﹣1=0
C. x2﹣2x﹣1=0 D. x2﹣2x+1=0
【答案】A
【解析】
【分析】根据一元二次方程根的判别式求解即可,一元二次方程![]() 的根的判别式
的根的判别式![]() ,
,![]() >0时,方程有两个不相等的实数根;
>0时,方程有两个不相等的实数根;![]() =0时,方程有两个相等的实数根;
=0时,方程有两个相等的实数根;![]() <0时,方程没有实数根.
<0时,方程没有实数根.
【详解】A. x2+x+1=0,![]()
![]() ,则原方程没有实数根,符合题意;
,则原方程没有实数根,符合题意;
B. x2+x﹣1=0,![]()
![]() ,则原方程有两个不相等的实数根,不符合题意;
,则原方程有两个不相等的实数根,不符合题意;
C. x2﹣2x﹣1=0,![]()
![]() ,则原方程没有实数根,不符合题意;
,则原方程没有实数根,不符合题意;
D. x2﹣2x+1=0,![]()
![]() ,则原方程有两个相等的实数根,不符合题意;
,则原方程有两个相等的实数根,不符合题意;
故选A
【点睛】本题考查了一元二次方程根的判别式,理解一元二次方程根的判别式是解题的关键.
10. 如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600cm2,设剪去小正方形的边长为xcm,则可列方程为( )
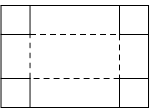
A. (30﹣2x)(40﹣x)=600 B. (30﹣x)(40﹣x)=600
C. (30﹣x)(40﹣2x)=600 D. (30﹣2x)(40﹣2x)=600
【答案】D
【解析】
【分析】设剪去小正方形的边长是xcm,则纸盒底面的长为(40﹣2x)cm,宽为(30﹣2x)cm,根据长方形的面积公式结合纸盒的底面积是600cm2,即可得出关于x的一元二次方程,此题得解.
【详解】解:设剪去小正方形的边长是xcm,则纸盒底面的长为(40﹣2x)cm,宽为(30﹣2x)cm,
根据题意得:(40﹣2x)(30﹣2x)=600.
故选:D.
【点睛】本题考查的是一元二次方程的应用,正确理解题意找到等量关系是解题的关键.
11. 关于函数y=36x2的叙述,错误的是( )
A. 图象的对称轴是y轴
B. 图象的顶点是原点
C. 当x>0时,y随x的增大而增大
D![]() y有最大值
y有最大值
【答案】D
【解析】
【分析】根据二次函数的性质得出函数y=36x2的对称轴及其增减性即可得出结论.
【详解】解:∵函数y=36x2的顶点在原点,
∴其对称轴是y轴,顶点是原点,故A、B正确;
∵函数y=36x2的开口向上,顶点是原点,
∴当x>0时,y随x的增大而增大,y有最小值,故C正确,D错误.
故选D.
【点睛】本题考查二次函数的性质,熟知二次函数y=ax2(a≠0)的顶点在原点,对称轴是y轴是解题的关键.
12. 用配方法解方程![]() ,变形后的结果正确的是( )
,变形后的结果正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】
【分析】先将常数项移到右侧,然后两边同时加上一次项系数一半的平方,配方后进行判断即可.
【详解】![]() ,
,
![]() ,
,
![]() ,
,
所以![]() ,
,
故选D.
【点睛】本题考查了配方法解一元二次方程,熟练掌握配方法的一般步骤以及注意事项是解题的关键.
13. 设一元二次方程![]() 的两根为
的两根为![]() ,
,![]() ,则
,则![]() 的值为( )
的值为( )
A. 1 B. ![]() C. 0 D. 3
C. 0 D. 3
【答案】A
【解析】
【分析】先利用一元二次方程根与系数的关系得![]() ,
,![]() ,然后利用整体代入的方法计算即可.
,然后利用整体代入的方法计算即可.
【详解】解:![]()
根据根与系数的关系得![]() ,
,![]() ,
,
![]()
![]()
![]()
![]() ,
,
故选:A.
【点睛】本题考查利用一元二次方程根与系数的关系求代数式的值,若![]() ,
,![]() 是一元二次方程
是一元二次方程![]() 的两根,则
的两根,则![]() ,
,![]() ,掌握一元二次方程根与系数的关系是解决问题的关键.
,掌握一元二次方程根与系数的关系是解决问题的关键.
第Ⅱ卷(非选择题)
二、填空题(本大题共6小题,共18.0分)
14. 方程x2=4的解是_____.
【答案】![]()
【解析】
【分析】直接运用开平方法解答即可.
【详解】解:∵x2=4
∴x=![]() =
=![]() .
.
故答案为x=![]() .
.
【点睛】本题主要考查了运用开平方法求解一元二次方程,牢记运用开平方法求的平方根而不是算术平方根是解答本题的关键,也是解答本题的易错点.
15. 写出顶点坐标为(0,-3),开口方向与抛物线![]() 的方向相反,形状相同的抛物线解析式_________________________.
的方向相反,形状相同的抛物线解析式_________________________.
【答案】![]()
【解析】
【分析】根据开口方向与抛物线![]() 的方向相反,形状相同可得
的方向相反,形状相同可得![]() ,再利用顶点坐标即可写出解析式.
,再利用顶点坐标即可写出解析式.
【详解】∵抛物线与![]() 的方向相反,形状相同,且顶点坐标(0,-3)
的方向相反,形状相同,且顶点坐标(0,-3)
∴设抛物线解析式为:![]() ,
,
代入顶点坐标(0,-3)得:![]()
∴解析式为![]()
故答案为![]() .
.
【点睛】本题考查求抛物线解析式,熟记抛物线顶点式是解题![]() 关键.
关键.
16. 某县2019年粮食总产量为100万吨,经过两年的努力,该县2021年粮食总产量达到121万吨,则该县这两年粮食总产量的年平均增长率为 __.
【答案】![]()
【解析】
【分析】设年平均增长率为![]() ,根据增长问题列出方程,解方程求出增长率.
,根据增长问题列出方程,解方程求出增长率.
【详解】设该县这两年粮食总产量的年平均增长率为![]() ,
,
根据题意得:![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
答:该县这两年粮食总产量的年平均增长率为![]() .
.
故答案为:![]() .
.
【点睛】本题考查一元二次方程的应用,掌握列方程解增长率问题是解题的关键.
17. 若二次函数的![]() 的图像经过点
的图像经过点![]() ,则
,则![]() _________.
_________.
【答案】![]()
【解析】
【分析】利用抛物线过点,则点的坐标满足解析式,把点代入即可.
【详解】二次函数![]() y=ax2的图像经过点(1,−2),
y=ax2的图像经过点(1,−2),
-2=a,
a=-2.
故答案为:-2.
【点睛】本题考查二次项系数问题,关键掌握图像经过点,点的坐标满足解析式使问题得以解决.
18. 把抛物线![]() 向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为________.
向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为________.
【答案】![]()
【解析】
【分析】根据“左加右减、上加下减”的平移原则进行解答即可.
【详解】解:抛物线![]() 向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为
向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为![]()
故答案为:![]() (或
(或![]() )
)
【点睛】本题考查了二次函数的平移,掌握函数平移规律是解题的关键.
19. 已知实数a、b满足![]() ,则代数式
,则代数式![]() 是否存在最小值______,最小值是______.
是否存在最小值______,最小值是______.
【答案】 ①. 存在 ②. 8
【解析】
【分析】根据![]() 得
得![]() ,代入
,代入![]() ,结合配方法,即可设二次函数
,结合配方法,即可设二次函数![]() ,根据二次函数的图象与性质即可作答.
,根据二次函数的图象与性质即可作答.
【详解】解:![]() ,
,
![]() ,
,
将![]() ,代入
,代入![]() ,
,
得![]() ,
,
设二次函数![]() ,
,
可知当![]() 时,函数值y随着a的增大而变大,
时,函数值y随着a的增大而变大,
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,函数值y取得最小值8,
时,函数值y取得最小值8,
即代数式![]() 存在最小值,最小值为8,
存在最小值,最小值为8,
故答案为:存在,8.
【点睛】本题考查了二次函数的最值问题,解题的关键是掌握二次函数的图象与性质.
三、解答题(本大题共7小题。解答应写出文字说明,证明过程或演算步骤)
20. 解下列方程:
(1)![]() ;
;
(2)![]()
【答案】(1)![]()
(2)![]()
【解析】
【分析】(1)根据直接开平方法解一元二次方程,即可求解;
(2)根据因式分解法解一元二次方程,即可求解.
【小问1详解】
解:![]() ,
,
即![]() ;
;
解得:![]() ,
,
【小问2详解】
解:![]() ,
,
∴![]() ,
,
即![]() ,
,
解得:![]() .
.
【点睛】本题考查了解一元二次方程,熟练掌握解一元二次方程的方法是解题的关键.
21. 解下列方程:
(1)![]() ;
;
(2)![]() .
.
【答案】(1)![]() ,
,![]()
(2)![]() ,
,![]()
【解析】
【分析】(1)采用因式分解法求解;
(2)采用因式分解法求解.
【小问1详解】
![]()
![]() ,
,
即![]() ,或者
,或者![]() ,
,
∴![]() ,
,![]() ;
;
【小问2详解】
![]()
![]()
![]() ,
,
即![]() ,或者
,或者![]() ,
,
∴![]() ,
,![]() .
.
【点睛】本题主要考查了运用因式分解法解一元二次方程的知识,掌握因式分解,是解答本题的关键.
22. 已知关于![]() 的方程
的方程![]() .
.
(1)若方程有两个实数根.求![]() 的取值范围;
的取值范围;
(2)若方程的一个根为![]() ,求方程的另一个根.
,求方程的另一个根.
【答案】(1)![]()
(2)![]()
【解析】
【分析】(1)根据一元二次方程根的判别式的意义,令![]() ,即可求解;
,即可求解;
(2)设方程的另一个根为![]() ,根据一元二次方程根与系数的关系,即可求解.
,根据一元二次方程根与系数的关系,即可求解.
【小问1详解】
解:依题意,![]()
解得:![]()
【小问2详解】
解:设方程的另一个根为![]() ,则
,则![]()
解得:![]() .
.
【点睛】本题考查了一元二次方程根的判别式的意义,以及一元二次方程根与系数的关系:若![]() 是一元二次方程
是一元二次方程![]() 的两根,
的两根,![]() ,
,![]() ,掌握一元二次方程根与系数的关系是解题的关键.当
,掌握一元二次方程根与系数的关系是解题的关键.当![]() 时,方程有两个不相等的实数根;当
时,方程有两个不相等的实数根;当![]() 时,方程有两个相等的实数根;当
时,方程有两个相等的实数根;当![]() 时,方程没有实数根.
时,方程没有实数根.
23. 新冠病毒的传染性极强,某地因1人患了新冠病毒没有及时隔离治疗,经过两天的传染后共有9人患了新冠病毒.
(1)每天平均一个人传染了几人?
(2)如果按照这个传染速度,再经过1天的传染后,这个地区一共将会有多少人患新冠病毒?
【答案】(1)2人 (2)27
【解析】
【分析】(1)设每天平均一个人传染了x人,根据“经过两天的传染后共有9人患了新冠病毒”列一元二次方程,求出x的值,即可求解;
(2)根据(1)的结果,直接计算即可.
【小问1详解】
解:设每天平均一个人传染了x人,
由题意,得![]() ,
,
整理得![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
即每天平均一个人传染了2人;
![]() 小问2详解】
小问2详解】
∵每天平均一个人传染了2人,现有9人已被感染,
∴第三天总患病人数为![]() (人),
(人),
答:再经过1天的传染后,这个地区一共将会有27人患新冠病毒.
【点睛】本题考查一元二次方程的实际应用,根据题意正确列出一元二次方程是解题的关键.
24. 已知二次函数![]() 图象的顶点坐标是
图象的顶点坐标是![]() ,且过点
,且过点![]() .
.
(1)求二次函数的解析式.
(2)当x为何值时,函数值y随x的增大而增大?
【答案】(1)![]()
(2)![]()
【解析】
【分析】(1)利用待定系数法即可求解;
(2)根据二次函数的图象与性质即可作答.
【小问1详解】
解:根据题意有: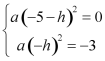 ,且
,且![]() ,
,
解得: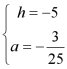 ,
,
即二次函数的解析式为:![]() ;
;
【小问2详解】
在二次函数![]() 中,
中,![]() ,对称轴为:
,对称轴为:![]() ,
,
∴抛物线开口朝下,
∴当![]() 时,函数值y随x的增大而增大.
时,函数值y随x的增大而增大.
【点睛】本题主要考查了二次函数的图象与性质,掌握二次函数的图象与性质,是解答本题的关键.
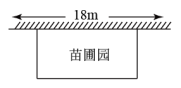
25. 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.若苗圃园的面积为72平方米,求x的值.
【答案】12
【解析】
【分析】根据题意,列出方程![]() 解得
解得![]() 由题可知
由题可知![]() 解得
解得![]() ,进而求出最后x的值.
,进而求出最后x的值.
【详解】解:由题意,得
![]()
解得![]()
又![]()
解得![]()
![]()
故答案为:12.
【点睛】本题考查一元二次方程与不等式的综合应用,熟练地解一元二次方程和不等式式解决问题的关键.
26. 已知关于x的一元二次方程x2﹣(2m+1)x+m(m+1)=0.
(1)求证:无论m取何值,方程总有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是这个方程的两个实数根,且BC=8,当△ABC为等腰三角形时,求m的值.
【答案】(1)详见解析;(2)当△ABC为等腰三角形时,m的值为7或8.
【解析】
【分析】(1)先根据题意求出△的值,再根据一元二次方程根的情况与判别式△的关系即可证得结论;(2)根据△ABC的两边AB、AC的长是这个方程的两个实数根,设AB=x1=8,代入得方程82﹣8(2m+1)+m(m+1)=0,解方程求出m的值即可.
【详解】解:(1)∵△=[﹣(2m+1)]2﹣4m(m+1)=1>0,
∴不论m为何值,方程总有两个不相等的实数根.
(2)由于无论m为何值,方程恒有两个不等实根,故若要△ABC为等腰三角形,那么必有一个解为8;
设AB=x1=8,则有:
82﹣8(2m+1)+m(m+1)=0,即:m2﹣15m+56=0,
解得:m1=7,m2=8.
则当△ABC为等腰三角形时,m![]() 值为7或8.
值为7或8.
【点睛】本题考查了一元二次方程根的情况与判别式△的关系:
(1)△>0⇔方程有两个不相等的实数根;
(2)△=0⇔方程有两个相等的实数根;
(3)△<0⇔方程没有实数根.