2022-2023学年广东深圳光明区七年级上册期中数学试卷及答案
注意事项:
1.答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上.
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点
涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.答案不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用涂改液.不按以上要求作答,视为无效.
4.考生必须保证答题卡的整洁.考试结束后,将答题卡交回.
第一部分 选择题
一.选择题(本大题共10小题,每小题3分,共30分.每小题给出4个选项,其中只有一个是正确的)
1. 如果将“收入50元”记作“+50元”,那么“支出20元”记作( )
A. +20元 B. ﹣20元 C. +30元 D. ﹣30元
【答案】B
2. 若a与-2互为相反数,则a的值是( )
A. -2 B. ![]() C.
C. ![]() D. 2
D. 2
【答案】D
3. 据科学家估计,地球的年龄大约是4 600 000 000年.则4 600 000 000用科学记数法可表示为( )
A. 46×108 B. 4.6×109 C. 4.6×1010 D. 0.46×1010
【答案】B
4. 如图,是一个正方体的展开图,原正方体与“队”字相对面上的字是( )
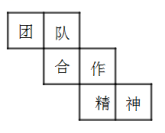
A. 合 B. 作 C. 精 D. 神
【答案】C
5. 下列各组数中,相等的一组是()
A. − 1 和 ( − 4) + ( − 3) B. | − 3| 和− ( − 3)
C![]() -|5| 和 |-5| D. -(-5) 和-|-5|
-|5| 和 |-5| D. -(-5) 和-|-5|
【答案】B
6. 下列几何体中,截面不可能是圆的是().
A. 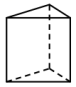 B.
B.  C.
C. 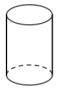 D.
D. 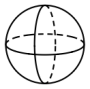
【答案】A
7. 若![]() ,则
,则![]() 的值为( )
的值为( )
A. 9 B. 1 C. -1 D. -4
【答案】C
8. 下列说法:(1)整数和分数统称为有理数;(2)任何有理数都有倒数;(3)一个数的绝对值一定为正数;(4)立方等于本身的数是1和-1.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】A
9. 某工厂1月份的产值为500万元,平均每月产值的增长率为x,则该工厂3月份的产值为()
A![]()
![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】B
10. 有理数a,b,c在数轴上对应的点如图所示,则下列结论中正确的有( )个
①a>b;②|b+c|=b+c;③|a﹣c|=c﹣a;④﹣b<c<﹣a.
![]()
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
第二部分 非选择题
二.填空题(本大题共5小题,每小题3分,共15分)
11. 用“![]() ”或“
”或“![]() ”连接:
”连接:![]() __
__![]() .
.
【答案】![]()
12. 在数轴上与![]() 的距离等于8的点表示的数是_____________.
的距离等于8的点表示的数是_____________.
【答案】-11或5##5或-11
13. 对任意四个有理数![]() ,
,![]() ,
,![]() ,
,![]() 定义新运算:
定义新运算:![]() ,则
,则![]() 的值为__.
的值为__.
【答案】![]()
14. 用棱长是1cm的小正方体组成如图所示的几何体,把这个几何体放在桌子上,并把暴露的面涂上颜色,那么涂颜色面的面积之和是________cm2.
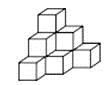
【答案】30
15. 已知![]() ,那么
,那么![]() 的值为____________.
的值为____________.
【答案】2024
三.解答题(本题共7小题,其中第16题12分,第17题6分,第18题6分,第19题6分,第20题7分,第21题8分,第22题10分,共55分)
16. 计算:
(1)![]()
(2)![]()
(3)![]()
(4)![]()
【答案】(1)1(2)15(3)4
(4)![]()
【分析】(1)根据有理数的加减混合运算法则计算即可;
(2)根据有理数![]() 乘除法混合运算法则计算即可;
乘除法混合运算法则计算即可;
(3)根据含乘方的有理数的混合运算求解即可;
(4)根据含乘方的有理数的混合运算求解即可.
【小问1详解】
解:![]()
![]()
![]() ;
;
【小问2详解】
![]()
![]()
![]() ;
;
【小问3详解】
![]()
![]()
![]()
![]() ;
;
【小问4详解】
![]()
![]()
![]() .
.
17. 若a、b互为相反数,c、d互为倒数,m的绝对值等于4,求:![]() 的值.
的值.
【答案】![]()
【分析】根据相反数,倒数和绝对值的定义得到![]() ,由此求解即可.
,由此求解即可.
【详解】解:∵a、b互为相反数,c、d互为倒数,m的绝对值等于4,
∴![]() ,
,
∴![]() .
.
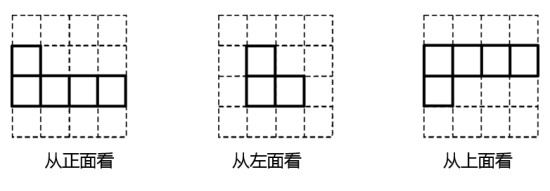
18. 如图,请分别画出从正面、左面和上面观察该几何体看到![]() 形状图.
形状图.
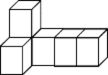

【答案】见解析
【分析】根据三视图的定义结合图形可得.
【详解】解:如图所示:
19. 已知有理数a,b,c在数轴上的位置如图所示.
![]()
(1)填空:a_______0,b_______0,a+c_______0(填“>”“<”或“=”);
(2)试化简:![]()
【答案】(1)>;<;<
(2)![]()
【分析】(1)根据题意得:c<b<0<a,且|c|>|a|,然后利用有理数的加法法则,进行计算即可解答;
(2)利用(1)的结论,先化简各式,然后再进行计算即可解答.
【小问1详解】
解:由题意得:
c<b<0<a,且|c|>|a|,
∴a>0,b<0,a+c<0,
故答案为:>;<;<;
【小问2详解】
解:∵c<b<0<a,
∴![]()
![]()
![]() .
.
20. 一辆汽车在一东西走向的街道上修路灯,以车站为出发点,向东走记为正,向西走记为负(单位:千米),以先后次序记录如下:-3,+4,-5,+10,+5,-8,-6,+7.试回答下列问题:
(1)最后一次修完路灯后,汽车在出发点的哪一边,距离出发点多远?
(2)如果汽车每走10千米耗油1升,汽车上的人修完路灯后,回出发点之前共用了多少油?
【答案】(1)汽车在出发点的东边,距离出发点4千米;
(2)回出发点之前共用了4.8升油.
【分析】(1)将记录的数字相加,根据结果即可做出判断;
(2)将各数的绝对值相加,除以10即可得到结果.
【小问1详解】
解:﹣3+(+4)+(﹣5)+(+10)+(+5)+(﹣8)+(﹣6)+(+7)=4(千米),
所以最后一次修完路灯后,汽车在出发点的东边,距离出发点4千米;
【小问2详解】
解:![]()
![]()
![]() (千米),
(千米),
![]() (升)
(升)
所以回出发点之前共用了4.8升油.
21. 观察下列等式:![]() ,
,![]() ,
,![]() ,将以上三个等式两边分别相加得:
,将以上三个等式两边分别相加得:![]() .
.
(1)猜想并写出:![]() = .
= .
(2)直接写出下列各式的计算结果:![]() = ;
= ;
(3)探究并计算:![]() .
.
【答案】(1)![]()
(2)![]()
(3)![]()
【分析】(1)根据已知的等式,从数字找规律,即可解答;
(2)利用得出的规律变形,进行计算即可解答;
(3)按照(2)的思路,将原式转化成![]() ,进行计算即可解答.
,进行计算即可解答.
【小问1详解】
解:由题意得:
![]() ,
,
故答案为:![]() ;
;
【小问2详解】
由题意得:![]()
![]()
![]()
![]() ,
,
故答案为:![]() ;
;
【小问3详解】
由题意得:![]()
![]()
![]()
![]()
=![]() .
.
22. 阅读材料:若点A、B在数轴上分别表示有理数a、b,A、B两点间的距离表示为AB,则AB=|a﹣b|或者AB=|b﹣a|.比如a=3,b=﹣2,则AB=|3﹣(﹣2)|或者AB=|(﹣2)﹣3|,所以式子|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.根据上述材料,解答下列问题:
(1)数轴上表示2和﹣3的两点之间的距离是;
(2)数轴上表示x和﹣2的两点之间的距离表示为;
(3)若|x﹣2|=3,则x=;
(4)若|x﹣3|+|x+1|=6,则x的值为;
(5)当x=____时,式子|x﹣3|+|x|+|x+1|的值最小.
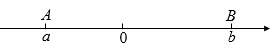
【答案】(1)5;(2)![]() ;(3)
;(3)![]() 或
或![]() ;(4)
;(4)![]() 或
或![]() ;(5)
;(5)![]()
【分析】(1)根据数轴上两点之间的距离,求解即可;
(2)根据数轴上两点之间的距离,求解即可;
(3)根据距离的含义,![]() 为到数2的点的距离为3的数,即可求解;
为到数2的点的距离为3的数,即可求解;
(4)根据距离的含义,![]() 为到数3的点的距离与到数-1的点的距离和为6的数,即可求解;
为到数3的点的距离与到数-1的点的距离和为6的数,即可求解;
(5)根据距离的含义,对![]() 进行分类讨论,分别求解即可.
进行分类讨论,分别求解即可.
【详解】解:(1)数轴上表示2和﹣3的两点之间的距离是![]()
故答案为5
(2)数轴上表示x和﹣2的两点之间的距离表示为![]()
故答案为![]()
(3)若|x﹣2|=3,![]() 为到数2的点的距离为3的数
为到数2的点的距离为3的数
∴![]() 或
或![]()
解得![]() 或
或![]()
故答案为![]() 或
或![]()
(4)若|x﹣3|+|x+1|=6,![]() 为到数3的点的距离与到数-1的点的距离和为6的数
为到数3的点的距离与到数-1的点的距离和为6的数
当![]() 时,
时,![]() ,
,![]() ,∴
,∴![]() ,解得
,解得![]()
当![]() 时,
时,![]() ,
,![]() ,∴
,∴![]() ,无解
,无解
当![]() 时,
时,![]() ,
,![]() ,∴
,∴![]()
解得![]()
综上所得,![]() 或
或![]()
(5)![]()
由(4)可得,当![]() 时,
时,![]() ,
,
∴![]() 的最小值时,
的最小值时,![]()
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
当![]() 时,
时,![]()
综上,当![]() 时,
时,![]() 的值最小,
的值最小,
故答案为![]()