2022－2023学年广东深圳龙华区七年级上册期末数学试卷及答案

说明：

1．试题卷共6页，答题卡共4页，考试时间90分钟，满分120分．

2．请在答题卡上填涂学校、班级、姓名，不得在其它地方作任何标记．

3．作答选择题1～10，每小题选出答案后，用2B铅笔将答题卷选择题答题区对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案；作答非选择题11～25，用黑色字迹的钢笔或签字笔将答案（含作辅助线）写在答题卷指定的答题区内，写在本卷或其他地方无效．

第一部分（选择题，共30分）

一、选择题（本题共有10小题，每小题3分，共30分，每小题有四个选项，其中只有一个是正确的）

1. 从正面观察如图所示的几何体，你所看到的几何体形状图是（　　）

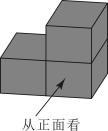
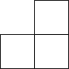A. B. C. D.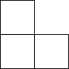

【答案】C

2. 2022年11月29日，神舟十五号载人飞船成功发射后，中国空间站以独特造型，由天和核心舱、问天实验舱、梦天实验舱以及两艘载人飞船和一艘货运飞船（天舟5号、神十四、神十五）组成“三舱三船”的组合体，这是中国空间站目前的最大构型，总质量近．数据100000用科学记数法表示为（　　）

A. B. C. D.

【答案】B

3. 下列各组整式中是同类项的是（　　）

A. 与 B. 与 C. 与 D. 与

【答案】D

4. 用一个平面去截下面几个几何体，截面不可能有圆的是（）

A. 圆锥 B. 圆柱 C. 棱柱 D. 球

【答案】C

5. 要调查下面的问题，适合用普查方式的是（　　）

A. 调查某一批西瓜是否甜 B. 调查我国七年级所有学生的视力情况

C. 调查某一批圆珠笔芯的使用寿命 D. 调查“力箭一号”运载火箭零部件的质量情况

【答案】D

6. 幻方的历史悠久，传说最早出现在夏禹时代的“洛书，把洛书用今天的数学符号翻译出来，就是一个三阶幻方．如图2所示，三阶幻方的每行、每列、每条对角线上的三个数之和相等．图3是另一个三阶幻方，则的值为（　　）

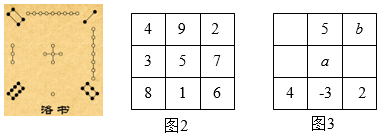
A. B. 2 C. 4 D.

【答案】A

7. 如图，，点、分别是线段上两点（，），用圆规在线段上分别截取，，若点与点恰好重合，则的长度为（　　）

A. 3 B. 4 C. 5 D. 6

【答案】C

8. 甲城市与乙城市的时差为两城市同一时刻的时数之差，如同一时刻北京为时，东京时间为，巴黎时间为，那么东京与北京的时差为，巴黎与北京的时差为．已知卡塔尔与北京的时差为，2022世界杯开幕式于北京时间2022年11月21日0时在卡塔尔卢塞尔体育场举行，此时卡塔尔卢塞尔的时间为（　　）

A. 11月20日05时 B. 11月20日19时 C. 11月21日05时 D. 11月21日19时

【答案】B

9. 小明和爸爸按相同的路径步行前往龙华书城，已知小明每步比爸爸少0.1米，他们的运动手环记录显示，小明去书城的路上走了4800步，爸爸走了4000步，请问小朋和爸爸每步各走多少米？设小明每步走米，则可列方程为（　　）

A. B.

C. D.

【答案】C

10. 如图，点是直线外一点，连接、，若点是直线上一动点，则下列说法正确的是（　　）

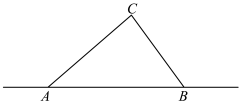
A. 点在射线上

B.

C. 连接，

D. 连接，若，则平分

【答案】D

第二部分（非选择题，共90分）

二、填空题（本题共有7小题，每小题4分，共28分．）

11. ﹣2的倒数是___．

【答案】

12. 点、在数轴上所表示的数如图所示，则、两点之间的距离是___________个单位长度．

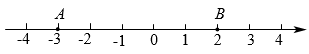
【答案】5

13. 单项式的系数是_______．

【答案】

14. 若是关于的方程的解，则___________．

【答案】3

15. 把如图所示的图形折叠成一个正方体的盒子，折好后相对面上的数互为相反数，则___________．

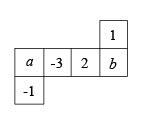
【答案】

16. 将连续的偶数2，4，6，8，10，…排成如图所示的数表，若将十字形框上下左右移动，可框出其中的五个数．当框住的五个数字之和为2030时，则位于十字形框中心的数为___________．

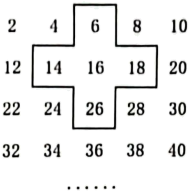
【答案】406

17. 乐乐同学有张长方形纸片折纸飞机，折叠过程如图所示，最后折成的纸飞机如图所示，则的度数为___________°．

【答案】45

三、解答题（一）（本题共3小题，共22分）

18. 计算：

（1）

（2）

【答案】（1）

（2）

【分析】（1）根据有理数的运算法则：先乘方，再乘除，最后再加减；有括号先算括号里面的；同级运算要从左到右；即可求解．

（2）先化简绝对值，再利用乘法分配律，即可求解．

【小问1详解】

解：原式

【小问2详解】

解：原式

19. 先化简、再求值：，其中，．

【答案】，

【分析】先化简整式，再将字母的值代入求解．

【详解】解：原式

；

当，时，

原式．

20. 解方程：

【答案】x=-1

【分析】去分母、去括号、移项、合并同类项、系数化为1，依此即可求解．

【详解】解：，

去分母得：3（1+x）-2（2x-1）=6，

去括号得：3+3x-4x+2=6，

移项得：3x-4x=6-3-2，

合并同类项得：-x=1，

系数化为1得：x=-1．

四、解答题（二）（本题共3小题，共21分）

21. 某校引进“A．麒麟舞，B．纸龙舞，C．鱼灯舞，D．醒狮舞”四个深圳市非物质文化遗产项目，为学生提供课后服务，要求每名学生必须且只能选定其中一个项目参加．在开学第一周，学校随机抽取部分学生进行了问卷调查，并将统计结果绘制出如图所示不完整的扇形统计图和条形统计图．请结合图中信息解答下列问题：

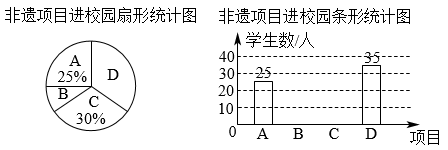
（1）此次被抽查的学生有___________人；

（2）在扇形统计图中，B所在的扇形的圆心角度数为___________°；

（3）补全图中的条形统计图；

（4）已知该校有3000学生，估计选定“D．醒狮舞”项目的人数为___________人．

【答案】（1）100（2）36

（3）见解析（4）1050

【分析】（1）已知选定项目的人数和人数占比，根据计算即可得到被调查的学生人数．

（2）根据扇形图，已知选定项目的人数占比，计算即可求出选定项目的人数，根据条形统计图可知选定项目的人数，计算即可知选定项目的人数和项目所对应的圆心角的度数．

（3）由（2）可得选定项目的人数，选定项目的人数，画出条形统计图即可．

（4）用该校学生总人数选定项目的人数占比即可得出答案．

【小问1详解】

（人）

被抽查的学生一共有100人．

【小问2详解】

（人），

（人），

，

故答案为：．

【小问3详解】

由（2）可得（人），（人），绘图如下：

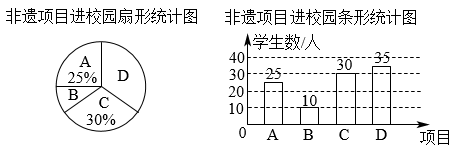【小问4详解】

（人），

故答案为：1050．

22. 列方程解决问题在“双11”促销活动中，某商场一运动品牌店实施如下调价方案：先把每件商品按原价提价50%后标价．又以6折销售．一套运动服经过上述调价后售价为270元．

（1）这套运动服的原价为多少元？

（2）在促销活动期间，乐乐妈妈到该品牌店购买了3套该运动服，所花的钱比调价方案前优惠了多少元？

【答案】（1）300元

（2）90元

【分析】（1）设这套运动服的原价为元，根据题意列方程求解即可；

（2）用优惠前的价格减去优惠后的价格乘以3，即可求解．

【小问1详解】

解：设这套运动服的原价为元，

依题意得：，

解得：，

答：这套运动服的原价为300元．

【小问2详解】

解：一套运动服调价后优惠了，

3套运动服比调价方案前优惠的总费用为．

23. 某节数学课后，小明同学在完成数学作业时，碰到了如下问题，请你跟小明一起来完成吧．

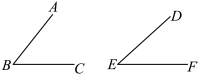
（1）比较图中与的大小：___________；（填“>”“＜“”或“=”）

（2）利用量角器画一个角，使得（点不在射线上）；

（3）利用能够画直角的工具（如直角三角板）画一个角，使得与共顶点，且．（保留画图痕迹）

【答案】（1）>（2）见解析

（3）见解析

【分析】（1）使用量角器分别量的两个角的度数，即可得到答案；

（2）用量角器量出的度数，再以为顶点，为边画出；

（3）利用直角三角板，以为顶点，为边画出直角，再以以为顶点，为边画出直角，同角的余角相等，则．

【小问1详解】

解：用量角器量得：，

故答案为：>；

【小问2详解】

用量角器量出的度数，再以为顶点，为边画出，如图所示：

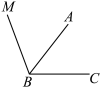【小问3详解】

利用直角三角板，以为顶点，为边画出直角，再以以为顶点，为边画出直角，则，如图所示：

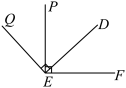
五、解答题（三）（本题共2小题，共19分）

24. 综合与实践

【问题背景】2022年10月23日是秋天最后的节气“霜降”，此时全国大多数地方都已入秋，但深圳还未入秋．因此某校七年级同学决定成立一个“调研小组”研究今年深圳的具体入秋日期．

【查阅资料】按天文角度划分标准：3～5月为春季、6～8月为夏季、9～11月为秋季、12月至翌年2月为冬季．

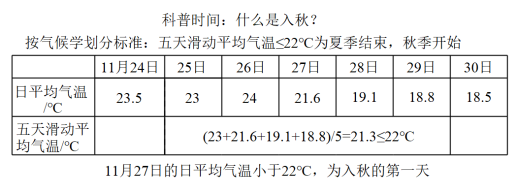
按气候学划分，深圳的入秋标准为：五天滑动平均气温≤22℃，从满足条件的五天中首个日平均气温≤22℃那天起算入秋（如图所示）．

【收集、整理数据】“调研小组”成员每天从“天气网”上收集当日气温，整理了2022年深圳连续20天的日平均气温，并以22℃为标准气温制定了如下表格：

日期	10.25	10.26	10.27	10.28	10.29	1030	10.31	11.1	11.2	11.3
日平均气温/℃	25	24.5	25.5	25	24.5	24	24	20.5	18.5	21
与标准气温差/℃	3	2.5	3.5	3	2.5	2	2
日期	11.4	115	11.6	11.7	11.8	11.9	11.10	11.12	11.13	11.14
日平均气温/℃	21.5	20.5		20	？	24	24	25.5	23.5	25.5
与标准气温的差/℃					？	2	2	3.5	1.5	3.5

【分析数据】

（1）表格中11月3日所在列的数字“”表示的意义是___________；

（2）已知11月8日平均气温比11月6日平均气温高3℃．

①11月8日的平均气温为___________℃；11月8日的气温与标准气温的差为___________℃．（请用含的代数式表示．）

②已知11月6日的平均气温与11月8日的平均气温之和为11月7日平均气温的2倍，请列出方程，求出的值．

（3）根据收集的气温数据及气候学划分标准，请通过计算说朋2022年深圳入秋的日期是哪天？

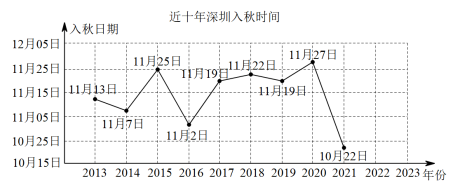
（4）根据第（3）小题中计算出的2022年入秋日期，补全下面的折线统计图；根据近十年深圳的入秋时间预估深圳市2023年的入秋时间，并说说你的理由．

【答案】（1）11月3日的平均气温比标准气温低1℃

（2）①；，②，18.5

（3）11月1日（4）补全统计图见解析，11月5日，理由见解析

【分析】（1）11月3日的平均气温比标准气温低1℃；

（2）①11月6日的气温为℃，则11月8日的平均气温为℃，11月8日的气温与标准气温的差为℃；

②根据题意列出方程求解即可；

（3）先计算10月30日至11月3日的平均气温，从满足条件的五天中找出首个日平均气温≤22℃的即可；

（4）由（3）得出的数据补全统计图，根据过去的数据预估2023年的入秋时间，这个时间为预估结果，因此无标准答案，只要把预估结果的理由说清即可．

【小问1详解】

解：11月3日的平均气温比标准气温低1℃；

故答案为：11月3日的平均气温比标准气温低1℃；

【小问2详解】

解：①11月6日的气温为℃，则11月8日的平均气温为℃，11月8日的气温与标准气温的差为℃；

故答案为：；；

②依题意得，

解得，

【小问3详解】

10月30日至11月3日的平均气温为：

，

又11月1日的平均气温为这5天中首个不超过22℃的一天，

2022年深圳入秋的日期为11月1日．

【小问4详解】

如图所示：

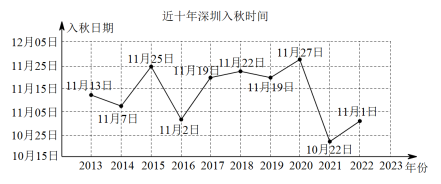
根据近10年深圳市的入秋时间，深圳常年入秋时间是在11月份，近10年的入秋平均日期为11月3日，预估2023年入秋时间为11月5日．

（说明：根据过去的数据预估2023年的入秋时间，这个时间为预估结果，因此无标准答案，只要把预估结果的理由说清即可．可以从平均数、中位数、区间值等方面说理皆可．）

25. 【定义】一个多元多项式（这里的“元”指的是多项式中的字母），如果把其中任意两个元互换，所得的结果都与原多项式相同，则称此多项式是关于这些元的对称多项式．如、都是关于元、、的对称多项式．

【理解】

（1）请根据上述对称多项式的概念，写出一个新的对称多项式___________．

【应用】

（2）请判断是否是对称多项式？并说明理由．

【拓展】

（3）两个任意的对称多项式的和或差一定是对称多项式吗？若是，请说明理由；若不是，请举出一个反例．

【答案】（1）

（2）不是，见解析（3）不是，见解析

【分析】（1）根据对称多项式概念求解即可；

（2）根据题意将x和y互换，然后根据对称多项式的概念求解即可；

（3）根据题意举例求解即可．

【小问1详解】

根据对称多项式的概念可得，

写出一个新的对称多项式为：，

故答案为：．

【小问2详解】

解：不是对称多项式，

理由如下：因为将原多项式中的与互换，新的多项式为：

所以

所以不是对称多项式；

【小问3详解】

不是，

如是关于元、的对称多项式，是关于元、、的对称多项式，

∴

∵不是对称多项式

∴两个任意的对称多项式的和或差不一定是对称多项式．