www.ks5u.com
2019年辽宁普通高中会考数学真题及答案
(本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分, 满分100分,考试时间90分钟)
参考公式：柱体体积公式 
，锥体体积公式 
（其中
为底面面积，
为高）； 球的表面积公式 
(其中
为球的半径)．
第I卷
一．选择题:（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1.集合
，则
（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
【分析】
直接利用并集的定义求解即可.
【详解】因为
，
所以
=
,故选D.
【点睛】研究集合问题，一定要抓住元素，看元素应满足的属性.研究两集合的关系时，关键是将两集合的关系转化为元素间的关系，本题实质求满足属于集合
或属于集合
的元素的集合.
2.函数
在区间[-2,-1]上的最大值是( )
A. 1 B. 2 C. 4 D. 
【答案】C
【解析】
【分析】
根据函数
的单调性，判断出当
时函数取得最大值，并由此求得最大值.
【详解】由于
为定义域上的减函数，故当
时函数取得最大值为
.故选C.
【点睛】本小题主要考查指数函数的单调性，考查指数运算，考查函数最值的求法，属于基础题.
3.函数
的最小正周期是（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
【分析】
根据
求得函数的最小正周期.
【详解】依题意可知，函数的最小正周期为
，故选B.
【点睛】本小题主要考查
的最小正周期计算，属于基础题.
4.已知
,则
的值是 （ ）
A. 0 B. –1 C. 1 D. 2
【答案】A
【解析】
【分析】
利用函数解析式，直接求出
的值.
【详解】依题意
.故选A.
【点睛】本小题主要考查函数值的计算，考查函数的对应法则，属于基础题.
5.如图所示，一个空间几何体的主视图和左视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的表面积为（ ）
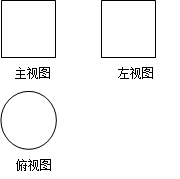
A. 
B. 
C. 
D. 
【答案】A
【解析】
【分析】
首先根据三视图得到几何体为圆柱，根据圆柱的表面积公式计算出表面积.
【详解】由三视图可知，该几何体为圆柱，故其表面积为
，故选A.
【点睛】本小题主要考查三视图还原为原图，考查圆柱的表面积计算公式，属于基础题.
6.已知向量
，向量
，若
，则实数
的值为（ ）
A. 
B. 3 C. 
D. 1
【答案】B
【解析】
【分析】
根据两个向量垂直的坐标表示列方程，由此求得
的值.
【详解】由于两个向量垂直，故
，故选B.
【点睛】本小题主要考查两个向量垂直的坐标表示，考查方程的思想，属于基础题.
7.在某次考试中，共有100个学生参加考试，如果某题的得分情况如表：
得分 | 0分 | 1分 | 2分 | 3分 | 4分 |
百分率 | 37.0 | 8.6 | 6.0 | 28.2 | 20.2 |
那么这些得分的众数是（ ）
A. 37.0% B. 20.2% C. 0分 D. 4分
【答案】C
【解析】
由题意得，得分为0分的比例为37.0%，所占比例最大，所以这些得分的众数是0。选C。
8.若回归直线的方程为
，则变量x 增加一个单位时 （ ）
A. y 平均增加1．5个单位 B. y 平均增加2个单位
C. y 平均减少1．5个单位 D. y 平均减少2个单位
【答案】C
【解析】
【分析】
根据回归直线方程
的斜率为负，可得出正确选项.
【详解】由于回归直线方程为
，其斜率为
，故变量
增加一个单位时，
平均减少
个单位.故选C.
【点睛】本小题主要考查对回归直线方程系数的理解，考查直线的斜率，属于基础题.
9.若直线
过点
且与直线
垂直，则
的方程为
A. 
B. 
C. 
D. 
【答案】A
【解析】
【分析】
根据所求直线与已知直线垂直可以求出斜率，再根据点斜式写出直线方程.
【详解】因为
的斜率
，所以
，由点斜式可得
，即所求直线方程为
，故选A.
【点睛】本题考查直线的位置关系及直线方程的点斜式，属于中档题.
10.已知
，
，若
，则点
的坐标为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
【分析】
设出
的坐标，代入
，计算出
点的坐标.
【详解】设
，则
，
，根据
得
，即
，解得
，故选D.
【点睛】本小题主要考查向量的减法和数乘计算，考查两个向量相等的坐标表示，属于基础题.
11.对于不同直线
以及平面
，下列说法中正确的是（ ）
A. 如果
，则
B. 如果
，则
C. 如果
,则
D. 如果
,则
【答案】D
【解析】
【分析】
根据线线、线面平行和垂直有关定理，对四个选项逐一分析，得出正确选项.
【详解】对于A选项，
可能含于
，故A选项错误.对于B选项，
两条直线可能异面，故B选项错误.对于C选项，
可能含于
，故C选项错误.对于D选项，根据线面垂直的性质定理可知，D选项正确，故选D.
【点睛】本小题主要考查线线、线面平行和垂直命题真假性的判断，考查线面垂直的性质定理，属于基础题.
12.等差数列{an}中，a2+a5+a8=12，那么函数
x2+（a4+a6）x+10零点个数为（ ）
A. 0 B. 1 C. 2 D. 1或2
【答案】C
【解析】
【分析】
根据等差数列的性质求得
的值，根据判别式判断出函数零点的个数.
【详解】根据等差数列的性质只
，
，故二次函数对应的判别式
，所以函数有两个零点，故选C.
【点睛】本小题主要考查等差数列的基本性质，考查二次函数零点和判别式的对应关系，属于基础题. 这个等差数列的性质是：若
，则
，若
，则
.如果数列是等比数列，则数列的性质为：若
，则
，若
，则
.所以解有关等差或者等比数列的题目时，先观察一下题目所给条件中的下标是否有关系.
第Ⅱ卷
二、填空题：本大题共4小题，每小题3分，共12分.
13.某超市有三类食品,其中果蔬类、奶制品类及肉制品类分别有20种、15种和10种, 现采用分层抽样的方法抽取一个容量为
的样本进行安全检测，若果蔬类抽取4种，则
为 ．
【答案】9
【解析】
【分析】
先根据果蔬类抽取的种类数计算出抽样的比例，乘以食品总的种类数得到样本容量
.
【详解】由果蔬类抽取
种可知，抽样比为
，故
.
【点睛】本小题主要考查分层抽样的知识和计算，考查运算求解能力，属于基础题.
14.圆C的方程是x2+y2+2x+4y=0，则圆的半径是_______________．
【答案】
【解析】
【分析】
将圆的一般方程配方，得到圆的标准方程，由此求得圆的半径.
【详解】依题意
，故圆的半径为
.
【点睛】本小题主要考查圆的一般方程化为标准方程，考查圆的半径的求法，属于基础题.
15.直线
的斜率是3，且过点A(1,-2),则直线
的方程是_____________．
【答案】
【解析】
【分析】
根据点斜式写出直线方程，并化为一般式.
【详解】由直线方程的点斜式得
，化简得
.
【点睛】本小题主要考查直线方程点斜式，考查点斜式转化为一般式，属于基础题.
16.若实数x，y满足
，则y的最大值是__________．
【答案】2．
【解析】
【分析】
画出可行域，根据图像判断出
的最大值.
【详解】画出可行域如下图所示，由图可知，
的最大值为
.
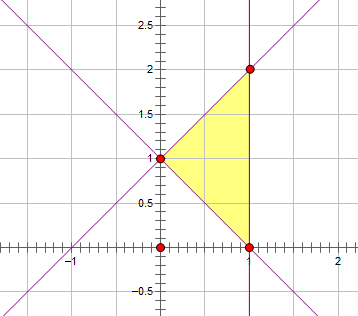
【点睛】本小题主要考查线性规划的知识，考查可行域的画法，属于基础题.
三、解答题：本大题共5小题，共52分.解答应写出文字说明、证明过程或演算步骤．
17.如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．
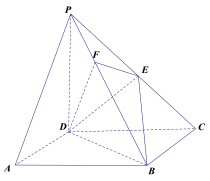
（Ⅰ）证明 PA//平面EDB；
（Ⅱ）证明PB⊥平面EFD.
【答案】(Ⅰ)详见解析；(Ⅱ)详见解析.
【解析】
【分析】
（I）连结
，
交
于
．连结
，通过中位线证明
，由此证得
平面
.（2）先证得
平面
，由此证得
，而
，故
平面
，由此证得
，结合
，可证得
平面
.
【详解】证明:（Ⅰ）连结
，
交
于
．连结
．∵底面
是正方形，∴点
是
的中点．在△
中，
是中位线，∴
//
．而
平面
，
且
平面
，所以，
//平面
．
（Ⅱ）∵
⊥底面
，且
底面
，∴
⊥
.
∵底面
是正方形，有
⊥
,
，
平面
，
平面
,∴
⊥平面
．而
平面
，∴
⊥
.
又∵
，
是
的中点，∴
⊥
，
，
平面
，
平面
.∴
⊥平面
．而
平面
，
∴
⊥
．又
⊥
，且
，
平面
，
平面
，所以
⊥平面
．
【点睛】本小题主要考查线面平行的证明，考查线面垂直的证明，属于中档题.
18.等差数列
中，
.
(1)求
的通项公式；
(2)设
，求数列
的前
项和
.
【答案】（I）
（II）
【解析】
(1)设等差数列{an}的公差为d，则an＝a1＋(n－1)d.
因为
所以
.
解得a1＝1，d＝
.所以{an}的通项公式为an＝
.
(2)bn＝
＝
，
所以Sn＝
19.已知
的三个内角A，B，C的对边分别为a，b，c.若
.
（1）求角C的大小；
（2）若
的面积为
，c=
，求
的周长.
【答案】（1）
；（2）
.
【解析】
【分析】
（1）由正弦定理可得a2+b2-c2=ab，再用余弦定理可得cosC,即可求得C；
（2）由面积公式可得ab=8，再结合余弦定理求得a+b=6，相加可得周长．
【详解】（1）由
及正弦定理，得a2+b2-c2=ab，
由余弦定理得
，
∵
，∴
.
（2）由（1）知
.
由
的面积为
得
，解得ab=8，
由余弦定理得
，
∴(a+b)2=36，a+b=6，
故
的周长为
.
【点睛】本题考查解三角形，涉及正余弦定理的应用和三角形的面积公式，属中档题．
20.已知圆
的圆心
在直线
上，且与
轴正半轴相切，点
与坐标原点
的距离为
.
（Ⅰ）求圆
的标准方程；
（Ⅱ）斜率存在的直线
过点
且与圆
相交于
两点，求弦长
的最小值.
【答案】(Ⅰ) 
；(Ⅱ) 
.
【解析】
【分析】
（I）设出圆心坐标，利用圆心和原点的距离列方程求得圆心坐标和半径，由此求得圆的标准方程.（II）利用点斜式设出直线
的方程，利用弦长公式求得弦长的表达式，根据表达式求得弦长的最小值.
【详解】解：（Ⅰ）由题可设
，半径
，
.
圆
与
轴正半轴相切
，
圆
的标准方程：
.
（Ⅱ）设直线
的方程：
，
点
到直线
的距离
，
弦长
，
当
时，弦长
的最小值
.
【点睛】本小题主要考查圆的标准方程的求解，考查直线和圆相交所得弦长公式，属于中档题.要求直线和圆相交所得弦有关的题目，可以有两种方式来求解，一个是联立直线方程和圆的方程，利用韦达定理来求解，一个是利用圆的几何性质，通过计算圆心到直线的距离
，然后利用
来求解.
21.已知函数
，
.
（Ⅰ）若
为偶函数，求
的值并写出
的增区间；
（Ⅱ）若关于
的不等式
的解集为
，当
时，求
的最小值；
（Ⅲ）对任意的
，
，不等式
恒成立，求实数
的取值范围.
【答案】(1) 
；增区间
.
(2) 
的最小值为
，取“
”时
.
(3) 
.
【解析】
分析：（Ⅰ）由偶函数的定义得
，求出
的值.再根据二次函数单调区间的判断方法，确定
的增区间；
（Ⅱ）根据已知条件结合韦达定理，求得
的值.再化简整理
的表达式，结合
和基本不等式即可得到答案.
（Ⅲ）先求出
区间上
，再将不等式
恒成立，转化为
上
恒成立问题，构造新函数
，得
恒成立，分类讨论求得参数
的值.
详解：解：（Ⅰ）
为偶函数，
，即
，解得
.
所以，函数
，对称轴
，增区间
（Ⅱ）由题知
∴
又∵
，∴
∴
，
即
的最小值为
，取“
”时
（Ⅲ）∵
时，
∴
在
恒成立
记
，（
）
①当
时，
由
，∴
②当
时，
由
，∴
③当
时，
由
，
综上所述，
的取值范围是
点睛：本题主要考查单调性和奇偶性，二次函数、一元二次方程和一元二次不等式之间的关系，基本不等式的应用，不等式恒成立问题，准确把握常见函数的性质、恒成立问题的求解方法和灵活运用分类讨论思想是解题关键.