2022-2023学年重庆市高三上学期11月月考数学试题及答案
数学测试卷满分150分,考试时间120分钟.
注意事项:
1. 答题前,考生务必将自己的准考证号、姓名填写在答题卡上.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致.
2. 回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,用0.5毫米的黑色墨水签字笔在答题卡上书写作答.若在试题卷上作答,答案无效.
3. 考试结束,考生必须将试题卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
【分析】利用对数函数的单调性解不等式得到集合![]() ,然后求交集即可.
,然后求交集即可.
【详解】![]() ,所以
,所以![]() ,即
,即![]() ,
,![]() ,
,![]() .
.
故选:C.
2. 已知向量![]() ,
,![]() ,
,![]() ,则实数
,则实数![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
【分析】首先求出![]() 的坐标,依题意
的坐标,依题意![]() ,根据数量积的坐标表示得到方程,解得即可.
,根据数量积的坐标表示得到方程,解得即可.
【详解】解:因为![]() ,
,![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() ,解得
,解得![]() .
.
故选:A
3. 设![]() 是定义域为R的函数,且“
是定义域为R的函数,且“![]() ,
,![]() ”为假命题,则下列命题为真的是( )
”为假命题,则下列命题为真的是( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]()
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
【答案】C
【解析】
【分析】根据含有一个量词的命题的真假关系即可求解.
【详解】因为命题“![]() ”为假命题,
”为假命题,
所以命题“![]() ”为真命题,
”为真命题,
故选:![]() .
.
4. 已知![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() ,则不等式
,则不等式![]() 的解集为( )
的解集为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】
【分析】首先判断![]() 时函数的单调性,并根据零点,求
时函数的单调性,并根据零点,求![]() 的解集,然后根据奇函数的性质,求函数在
的解集,然后根据奇函数的性质,求函数在![]() 时,
时,![]() 的解集,即可求解.
的解集,即可求解.
【详解】当![]() 时,
时,![]() 是增函数+增函数=增函数,且
是增函数+增函数=增函数,且![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
根据奇函数![]() 性质可知,
性质可知,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以不等式![]() 的解集是
的解集是![]() .
.
故选:D
5. 设![]() ,函数
,函数![]() 为偶函数,则
为偶函数,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
【分析】利用辅助角公式化简![]() 得
得![]() ,然后根据偶函数得到
,然后根据偶函数得到![]() ,解得
,解得![]() ,最后根据
,最后根据![]() 即可得到
即可得到![]() 的最小值.
的最小值.
【详解】![]() ,因为
,因为![]() 为偶函数,所以
为偶函数,所以![]() ,故
,故![]() ,又
,又![]() ,最小值为
,最小值为![]() .
.
故选:D.
6. 设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
【分析】根据数列![]() 为等差数列,利用求和公式求得首项与公差,进而可得
为等差数列,利用求和公式求得首项与公差,进而可得![]() .
.
【详解】由数列![]() 为等差数列,则
为等差数列,则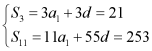 ,
,
解得![]() ,
,
则![]() ,
,
解得![]() 或
或![]() ,
,
又![]() ,所以
,所以![]() ,
,
故选:B.
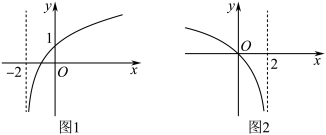
7. 已知函数![]() 的图象如图1所示,则图2所表示的函数是( )
的图象如图1所示,则图2所表示的函数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
【分析】根函数图象判断两个函数见的位置关系,进而可得解.
【详解】由图知,将![]() 的图象关于
的图象关于![]() 轴对称后再向下平移
轴对称后再向下平移![]() 个单位即得图2,
个单位即得图2,
又将![]()
![]() 图象关于
图象关于![]() 轴对称后可得函数
轴对称后可得函数![]() ,
,
再向下平移![]() 个单位,可得
个单位,可得![]()
所以解析式为![]() ,
,
故选:C.
8. 已知![]() ,且
,且![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
【分析】根据换底公式,找出![]() 的关系,再用“1”的代换,求出最小值.
的关系,再用“1”的代换,求出最小值.
【详解】解:由题知![]() ,
,
根据换底公式该等式可化![]()
![]()
![]() ,
,
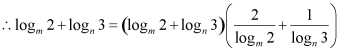
![]() ,
,
当且仅当![]() 时成立
时成立
![]() 最小值为
最小值为![]() .
.
故选:D
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 设![]() 是非零复数,则下列说法正确的是( )
是非零复数,则下列说法正确的是( )
A. 若![]() ,则
,则![]() B. 若
B. 若![]() ,则
,则![]()
C. 若![]() ,则
,则![]() D. 若
D. 若![]() ,则
,则![]()
【答案】ABD
【解析】
【分析】根据复数的运算性质逐一检验即可.
【详解】A选项,![]() ,故
,故![]() ,正确;
,正确;
B选项,![]() 即
即![]() .故
.故![]() ,正确;
,正确;
C选项,![]() 即z为纯虚数,故
即z为纯虚数,故![]() ,不正确;
,不正确;
D选项,∵![]() ,故
,故![]() ,正确.
,正确.
故选:ABD.
10. 已知![]() ,
,![]() ,则( )
,则( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】BC
【解析】
【分析】根据指数函数,对数函数,幂函数的单调性结合不等式的性质逐项分析即得.
【详解】A选项,∵![]() ,∴
,∴![]() 单调递增,∴
单调递增,∴![]() ,故A错误;
,故A错误;
B选项,由![]() 可知函数
可知函数![]() 单调递增,又
单调递增,又![]() ,
,
故![]() ,∴
,∴![]() ,即
,即![]() ,故B正确;
,故B正确;
C选项,由题可知![]() ,
,![]() ,
,![]() ,故
,故![]() ,即
,即![]() ,故C正确;
,故C正确;
D选项,函数![]() 单调递减,
单调递减,![]() 单调递增,
单调递增,![]() ,故
,故![]() ,故D错误.
,故D错误.
故选:BC.
11. 已知函数![]() 的最小正周期为
的最小正周期为![]() ,
,![]() ,且
,且![]() 是
是![]() 的一个极小值点,则( )
的一个极小值点,则( )
A. ![]()
B. 函数![]() 在区间
在区间![]() 上单调递减
上单调递减
C. 函数![]() 的图象关于点
的图象关于点![]() 中心对称
中心对称
D. 函数![]() 的图象与直线
的图象与直线![]() 恰有三个交点
恰有三个交点
【答案】ABD
【解析】
【分析】根据题意和三角函数的周期性求出![]() ,即可判断A;根据极小值的概念和正弦函数的图象与性质可知函数在[
,即可判断A;根据极小值的概念和正弦函数的图象与性质可知函数在[![]() ,π]上单减,即可判断B;利用验证法即可判断C;作出函数
,π]上单减,即可判断B;利用验证法即可判断C;作出函数![]() 与直线
与直线![]() 的部分图象,结合数形结合的思想即可判断D.
的部分图象,结合数形结合的思想即可判断D.
【详解】A:由题知![]() ,∴
,∴![]() ,
,
又![]() .
.![]()
![]() ,得
,得![]() ,故A正确;
,故A正确;
B:由![]() 为极小值点,
为极小值点,![]() ,∴f(x)在[
,∴f(x)在[![]() ,π]上单减,故B正确;
,π]上单减,故B正确;
C:![]() ,故(
,故(![]() ,0)不是f(x)的对称中心,故C错误;
,0)不是f(x)的对称中心,故C错误;
D:函数![]() 与直线
与直线![]() 的部分图象如下.
的部分图象如下.
直线![]() x恰好经过
x恰好经过![]() 的一个最低点(-
的一个最低点(-![]() ,-1),
,-1),
且当![]() 时,
时,![]() 或
或![]() ,
,
此时它与![]() 的图象再无交点,所以二者共有3个交点,故D正确.
的图象再无交点,所以二者共有3个交点,故D正确.
 .
.
故选:ABD.
12. 在![]() 中,
中,![]() ,
,![]() ,
,![]() 为内角
为内角![]() ,
,![]() ,
,![]() 的对边,
的对边,![]() ,记
,记![]() 的面积为
的面积为![]() ,则( )
,则( )
A. ![]() 一定是锐角三角形 B.
一定是锐角三角形 B. ![]()
C. 角![]() 最大为
最大为![]() D.
D. ![]()
【答案】BCD
【解析】
【分析】举例说明即可判断A;根据椭圆的定义和几何性质即可判断B;利用余弦定理求出![]() 即可判断C;根据正弦定理,结合三角恒等变换计算化简即可判断D.
即可判断C;根据正弦定理,结合三角恒等变换计算化简即可判断D.
【详解】A选项,取![]() ,但△ABC显然为直角三角形,故A错误;
,但△ABC显然为直角三角形,故A错误;
B选项,由![]() ,以A,C为焦点、2b为长轴长的椭圆上运动,
,以A,C为焦点、2b为长轴长的椭圆上运动,
结合椭圆的几何性质知,当B为短轴端点时△ABC面积最大,
且为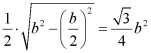 ,故B正确;
,故B正确;
C选项,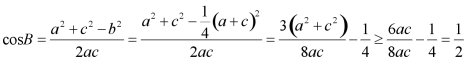 ,
,
当且仅当![]() 时取等号,故
时取等号,故![]() ,故C正确;
,故C正确;
D选项,![]() ,
,
![]() ,
,
![]() ,
,
显然![]() ,故
,故![]() ,
,
即![]() ,即
,即![]() ,故D正确.
,故D正确.
故选:BCD.
三、填空题:本题共4小题,每小题5分,共20分.
13. 曲线![]() 在点
在点![]() 处的切线方程为___________.
处的切线方程为___________.
【答案】![]()
【解析】
【分析】求导,根据导数的几何意义可得切线斜率,进而可得切线方程.
![]() 详解】由
详解】由![]() ,得
,得![]() ,
,
则![]() ,
,
又![]() ,
,
所以切线方程为![]() ,即
,即![]() ,
,
故答案为:![]() .
.
14. 已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() ,则
,则![]() ___________.
___________.
【答案】![]() ##
##![]()
【解析】
【分析】根据题意可得![]() ,进而求得
,进而求得![]() ,即可求解.
,即可求解.
【详解】设等比数列的公比为q,由![]() ,
,
得![]() ,
,
故![]() ,
,
所以![]() .
.
故答案为:![]() .
.
15. 已知向量![]() ,
,![]() 满足
满足![]() ,
,![]() ,
,![]() ,则
,则![]() 在
在![]() 上的投影向量的模为___________.
上的投影向量的模为___________.
【答案】1
【解析】
【分析】根据题意求出向量![]() 与向量
与向量![]() 的数量积,再根据公式即可求解.
的数量积,再根据公式即可求解.
【详解】因为向量![]() 满足
满足![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() 在
在![]() 上的投影向量的模为
上的投影向量的模为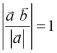 ,
,
故答案为:![]() .
.
16. 已知![]() 且
且![]() ,函数
,函数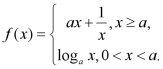 有最小值,则
有最小值,则![]() 的取值范围是___________.
的取值范围是___________.
【答案】![]()
【解析】
【分析】根据对数函数的性质可得当![]() 时函数无最小值,不符合题意;当
时函数无最小值,不符合题意;当![]() 时,利用基本不等式求出
时,利用基本不等式求出![]() 在
在![]() 上的最小值
上的最小值![]() ,利用对数函数的性质求出
,利用对数函数的性质求出![]() 在
在![]() 上的值域为
上的值域为![]() ,列出不等式
,列出不等式![]() ,解之即可.
,解之即可.
【详解】当![]() 时,
时,![]() x在(0,a)上单调递增,所以值域为(-∞,1),
x在(0,a)上单调递增,所以值域为(-∞,1),
故函数f(x)无最小值,不符合题意;
当![]() 时,
时,![]() 上有
上有![]() ,
,
所以![]() ,当且仅当
,当且仅当![]() 即
即![]() 时等号成立,
时等号成立,
所以![]() 的最小值为
的最小值为![]()
![]() x在(0,a)上单调递减,所以值域为(1,+∞),
x在(0,a)上单调递减,所以值域为(1,+∞),
故函数f(x)有最小值只需![]() ,即
,即![]() ,所
,所![]() .
.
故答案为:![]() .
.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 已知等差数列![]() 满足
满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 是公比为2的等比数列,且
是公比为2的等比数列,且![]() ,求数列
,求数列![]() 的前
的前![]() 项和.
项和.
【答案】(1)![]()
(2)![]()
【解析】
【分析】(1)设出等差数列![]() 的通项公式
的通项公式![]() ,根据题干条件列出方程,求出
,根据题干条件列出方程,求出![]() ,得到通项公式;
,得到通项公式;
(2)根据等比数列的定义得到![]() ,利用等差数列和等比数列求和公式,分组求和求出答案.
,利用等差数列和等比数列求和公式,分组求和求出答案.
【小问1详解】
设等差数列{![]() }的通项公式为
}的通项公式为![]() ,
,
则![]() ,故
,故![]() ,
,
即![]() ,
,
∴![]() :
:
【小问2详解】
![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
18. 已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
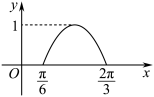
(1)求![]() 的解析式;
的解析式;
(2)求不等式![]() 的解集.
的解集.
【答案】(1)![]()
(2)![]()
【解析】
【分析】(1)根据图像判断周期,找出![]() ,根据零点代入解析式找出
,根据零点代入解析式找出![]() 即可.
即可.
(2)结合![]() 图像写出解集,化简即可.
图像写出解集,化简即可.
【小问1详解】
解:由图知![]() ,
,![]() ,
,
由图知![]() ,
,
故![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
【小问2详解】
由题知,![]() ,即
,即![]() ,
,
即![]() ,
,
解得![]() ,
,
故不等式的解集为![]() .
.
19. 如图,在平面四边形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
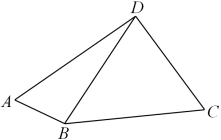
(1)求![]() ;
;
(2)若![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]()
(2)![]()
【解析】
【分析】(1)由已知结合同角的平方关系先求出![]() ,然后根据三角形内角和及两角和的正弦公式即可求解;
,然后根据三角形内角和及两角和的正弦公式即可求解;
(2) 在![]() 中,由正弦定理求出
中,由正弦定理求出![]() ,再结合诱导公式和三角形的面积公式q求出
,再结合诱导公式和三角形的面积公式q求出![]() ,然后利用勾股定理即可求解.
,然后利用勾股定理即可求解.
【小问1详解】
由题知![]() ,故
,故![]() ,.
,.
∴![]() ,
,
故![]() .
.
【小问2详解】
在![]() 中,由正弦定理得
中,由正弦定理得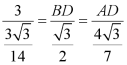 ,
,
即![]() 由
由![]() 知
知![]() ,
,
故![]() ,∴
,∴![]() ,∴
,∴![]() .
.
20. 已知函数![]() ,
,![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析
(2)![]()
【解析】
【分析】(1)先求导,再分![]() ,
,![]() ,
,![]() 讨论即可求解;
讨论即可求解;
(2)![]() 即
即![]() ,结合(1)即可求解
,结合(1)即可求解
【小问1详解】
![]() ,
,
当![]() 即
即![]() 时,
时,![]() 或
或![]() ,
,
故![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 即
即![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 即
即![]() 时,
时,![]() 或
或![]() ,
,
故![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
综上可知:![]() 时,故
时,故![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
![]() 时,
时,![]()
![]()
![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
【小问2详解】
由(1)知,当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,![]() 单调递增,
单调递增,
故![]() ,符合题意:
,符合题意:
当![]() 时,
时, ![]() ,
,
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
![]() ,
,
故![]() ,解得
,解得![]() ;
;
综上![]() .
.
21. 已知![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,函数
,函数![]() 的最大值为
的最大值为![]() .
.
(1)求![]() 的值;
的值;
(2)此![]() 是否能同时满足
是否能同时满足![]() ,且___________?
,且___________?
在①![]() ,②
,②![]() 边的中线长为
边的中线长为![]() ,③
,③![]() 边的高线长为
边的高线长为![]() 这三个条件中任选一个,补充在上面问题中,若
这三个条件中任选一个,补充在上面问题中,若![]() 满足上述条件,求其周长;若不能满足,请说明理由.
满足上述条件,求其周长;若不能满足,请说明理由.
【答案】(1)![]()
(2)选①,![]() 的周长为
的周长为![]() ;选②,
;选②,![]() 不存在,理由见解析;选③,
不存在,理由见解析;选③,![]() 的周长为
的周长为![]()
【解析】
【分析】(1)根据三角恒等变换化简函数解析式,根据函数的最值可得解;
(2)若选①,结合三角恒等变换可得![]() 的值,根据正弦定理可求得
的值,根据正弦定理可求得![]() ,再根据余弦定理可得
,再根据余弦定理可得![]() ,进而可判断是否成立并求得周长;若选②,由已知可得
,进而可判断是否成立并求得周长;若选②,由已知可得![]() ,根据
,根据![]() ,结合余弦定理可得
,结合余弦定理可得![]() 与
与![]() ,可得不成立;若选③,根据三角形面积可得
,可得不成立;若选③,根据三角形面积可得![]() ,再根据余弦定理可得
,再根据余弦定理可得![]() ,进而可判断是否成立并求得周长.
,进而可判断是否成立并求得周长.
【小问1详解】
![]()
![]()
![]() ,其中
,其中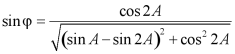 ,
,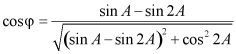 ,
,
又函数![]() 的最大值为
的最大值为![]() ,即
,即![]() ,
,
整理得![]() ,
,
又![]() ,
,
所以![]() ,
,
所以![]() ,
,
解得![]() ;
;
【小问2详解】
若选①,由![]() ,
,
即![]() ,得
,得![]() ,
,
又由正弦定理得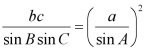 ,且
,且![]() ,
,
所以![]() ,
,
由余弦定理可知![]() ,解得
,解得![]() ,
,
且满足![]() ,所以
,所以![]() 满足条件,
满足条件,
![]() ,解得
,解得![]() ,
,
故![]() 的周长为
的周长为![]() ;
;
若选②,设![]() 边的中线为
边的中线为![]() ,则
,则![]() ,
,
所以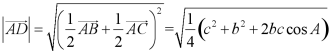 ,
,
所以![]() ,
,
又由余弦定理得![]() ,即
,即![]() ,
,
解得![]() ,
,![]() ,不满足
,不满足![]() ,
,
所以![]() 不存在;
不存在;
若选③,由三角形面积公式得![]() ,且
,且![]() ,
,
可得![]() ,
,
由余弦定理![]() ,
,
解得![]() ,满足
,满足![]() ,
,
所以![]() 满足上述条件,
满足上述条件,
![]() ,即
,即![]() ,
,
所以![]() 的周长为
的周长为![]() .
.
22. 已知函数![]() ,
,![]() .
.
(1)当![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(2)若![]() 存在两个极值点,求
存在两个极值点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
(2)![]()
【解析】
【分析】(1)求导,根据导数的符号即可求出函数的单调区间;
(2)求导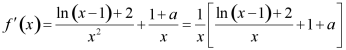 ,函数
,函数![]() 有两个极值点,则函数
有两个极值点,则函数![]() 至少有两个零点,构造函数
至少有两个零点,构造函数![]() ,利用导数求出函数的单调区间,作出函数
,利用导数求出函数的单调区间,作出函数![]() 的简图,数形结合从而可得出答案.
的简图,数形结合从而可得出答案.
【小问1详解】
解:![]() ,定义域为
,定义域为![]() ,
,
则![]() ,
,
![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
【小问2详解】
解: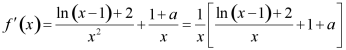 ,
,
函数![]() 有两个极值点,则函数
有两个极值点,则函数![]() 至少有两个零点,
至少有两个零点,
设![]() ,则
,则![]() ,
,
设![]() ,则
,则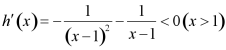 ,
,
所以函数![]() 在
在![]() 上递减,
上递减,
又![]() ,则
,则![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上递增,在
上递增,在![]() 递减,
递减,
又![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
欲使![]() 在
在![]() 内至少存在两个不等实根,
内至少存在两个不等实根,
则函数![]() 与
与![]() 在
在![]() 至少有两个交点,
至少有两个交点,
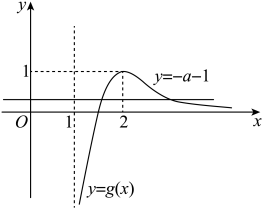
作出函数![]() 的图象,如图所示,
的图象,如图所示,
则![]() ,解得
,解得![]() ,
,
此时,![]() 在
在![]() 和
和![]() 内各存在一个零点,分别设为
内各存在一个零点,分别设为![]() ,
,
则![]() 或
或![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
故![]() 为
为![]() 的极小值点,
的极小值点,![]() 为
为![]() 的极大值点,符合题意,
的极大值点,符合题意,
所以![]() .
.
【点睛】本题考查了利用导数求函数的单调区间及函数的极值点、零点问题,考查了转化思想及数形结合思想,解决第二问的关键在于将问题转化为导函数至少有两个零点,有一定的难度.