2020年青海普通高中会考数学真题及答案
1. (2分) 已知集合A={x|x2﹣x﹣2<0},B={x| ![]() ≥﹣1},则A∪B=( )
≥﹣1},则A∪B=( )
A . (﹣1,2)
B . (﹣1,2]
C . (0,1)
D . (0,2)
2. (2分) 函数![]() 的最大值为( )
的最大值为( )
A . ![]()
B . ![]()
C . ![]()
D . ![]()
3. (2分) 函数y= ![]() sin2x+cos2x的最小正周期为( )
sin2x+cos2x的最小正周期为( )
A . ![]()
B . ![]()
C . π
D . 2π
4. (2分)若函数f( x)=ax3﹣bx+c为奇函数,则c=( )
A . 0
B . 1
C . ﹣1
D . ﹣2
5. (2分) 某几何体的三视图如图所示,当xy最大时,该几何体的体积为( )
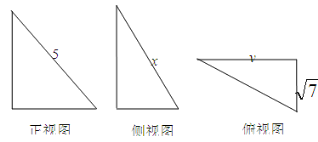
A . ![]()
B . ![]()
C . ![]()
D . ![]()
6. (2分) 已知 ![]() ,若
,若 ![]() ,则m=( )
,则m=( )
A . - ![]()
B . ﹣2
C . ![]()
D . 2
7. (2分) 某设计运动员在一次测试中射击10次,其测试成绩如表:则该运动员测试成绩的中位数为( )
环数 | 7 | 8 | 9 | 10 |
频数 | 3 | 2 | 2 | 3 |
A . 2
B . 8
C . 8.5
D . 9
8. (2分) 下表是x与y之间的一组数据,则y关于x的线性回归直线必过点( )
x | 0 | 1 | 2 | 3 |
y | 1 | 3 | 5 | 7 |
A . ![]()
B . ![]()
C . ![]()
D . ![]()
9. (2分) 已知A、B两点分别在两条互相垂直的直线y=2x和x+ay=0上,且线段AB的中点为P(0, ![]() ),则直线AB的方程为( )
),则直线AB的方程为( )
A . y=- ![]() x+5
x+5
B . y= ![]() x-5
x-5
C . y= ![]() x+5
x+5
D . y=- ![]() x-5
x-5
10. (2分) 平面直角坐标系中O是坐标原点,已知两点A(2,-1),B(-1,3),若点C满足![]() 其中
其中![]() 且
且![]() , 则点C的轨迹方程为( )
, 则点C的轨迹方程为( )
A . ![]()
B . ![]()
C . ![]()
D . ![]()
11. (2分) 三棱锥![]() 中,
中,![]() 分别是
分别是![]() 的中点,则四边形
的中点,则四边形![]() 是( )
是( )
A . 菱形
B . 矩形
C . 梯形
D . 正方形
12. (2分)已知函数 ![]() 若a,b,c均不相等,且
若a,b,c均不相等,且 ![]() ,则abc的取值范围是
,则abc的取值范围是
A . (1,10)
B . (5,6)
C . (10,12)
D . (20,24)
二、 填空题 (共4题;共4分)
13. (1分)某校老年教师90人、中年教师180人和青年教师160人,采用分层抽样的方法调查教师的身体情况,在抽取的样本中,青年教师有32人,则该样本的老年教师人数为________.
14. (1分) 圆(x+2)2+(y+3)2=1关于原点对称的圆的方程是________.
15. (1分)已知点A(1,2)、B(3,1),则线段AB的垂直平分线的方程是________.
16. (1分) 若变量x,y满足约束条件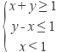 , 则z=2x﹣y的最小值为________
, 则z=2x﹣y的最小值为________
三、 解答题 (共5题;共35分)
17. (5分)如图所示,在四面体 ![]() 中,
中, ![]() ,平面
,平面 ![]() 平面
平面 ![]() ,
, ![]() ,且
,且 ![]() .
.
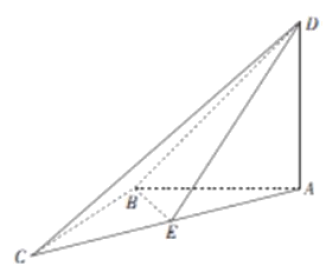
(1) 证明: ![]() 平面
平面 ![]() ;
;
(2) 设 ![]() 为棱
为棱 ![]() 的中点,当四面体
的中点,当四面体 ![]() 的体积取得最大值时,求二面角
的体积取得最大值时,求二面角 ![]() 的余弦值.
的余弦值.
18. (10分)已知公差大于零的等差数列{an}的前n项和Sn , 且满足a3·a5=112,a1+a7=22.
(1) 求等差数列{an}的第七项a7和通项公式an;
(2) 若数列{bn}的通项bn=an+an+1,{bn}的前n项和Sn,写出使得Sn小于55时所有可能的bn的取值.
19. (10分) 已知f(x)=cosxsinx﹣ ![]() cos2x+
cos2x+ ![]() .
.
(1) 求f(x)的单调增区间;
(2) 在△ABC中,A为锐角且f(A)= ![]() ,D为BC中点,AD=3,AB=
,D为BC中点,AD=3,AB= ![]() ,求AC的长.
,求AC的长.
20. (5分) 已知圆 ![]() 过圆
过圆 ![]() 与直线
与直线 ![]() 的交点,且圆
的交点,且圆 ![]() 上任意一点关于直线
上任意一点关于直线 ![]() 的对称点仍在圆
的对称点仍在圆 ![]() 上.
上.
(1) 求圆 ![]() 的标准方程;
的标准方程;
(2) 若圆 ![]() 与
与 ![]() 轴正半轴的交点为
轴正半轴的交点为 ![]() ,直线
,直线 ![]() 与圆
与圆 ![]() 交于
交于 ![]() 两点(异于点
两点(异于点 ![]() ),且点
),且点 ![]() 满足
满足 ![]() ,
,![]() ,求直线
,求直线 ![]() 的方程.
的方程.
21. (5分) 已知函数f(x)对任意x,y∈R,总有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,f(1)=- ![]() .
.
(1) 求证:f(x)是R上的单调减函数.
(2) 求f(x)在[-3,3]上的最小值.
参考答案
一、 单选题 (共12题;共24分)
1-1、![]()
2-1、![]()
3-1、![]()
4-1、![]()
5-1、![]()
6-1、![]()
7-1、![]()
8-1、![]()
9-1、![]()
10-1、![]()
11-1、![]()
12-1、![]()
二、 填空题 (共4题;共4分)
13-1、![]()
14-1、![]()
15-1、![]()
16-1、![]()
三、 解答题 (共5题;共35分)
17-1、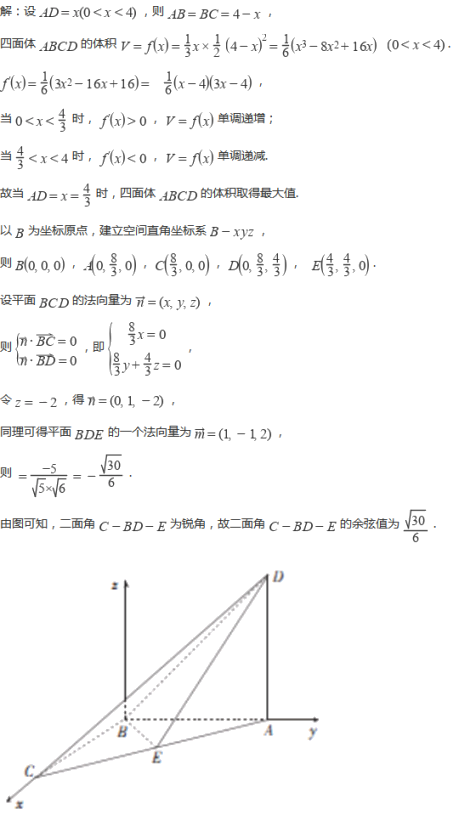

17-2、
18-1、
18-2、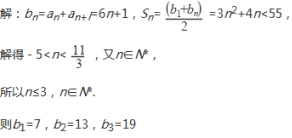
19-1、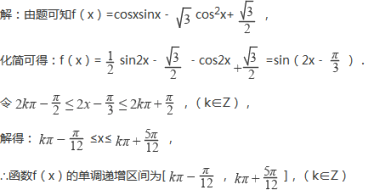
19-2、
20-1、
20-2、
21-1、
21-2、