1. （4分） 若不等式组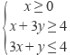所表示的平面区域被直线分为面积相等的两部分，则k的值是 （ ）                 

A .     

B .     

C .     

D .     

2. （4分） 已知O为△ABC所在平面内一点,满足

,则点O是△ABC的（ ）

A . 外心    

B . 内心    

C . 垂心    

D . 重心    

3. （4分） 函数y=lgx-1的零点是（ ）

A . 0    

B . 1    

C . 10    

D . （10，0）    

4. （4分） 不等式（x-3）（x-5）<0的解集是（ ）

A . （-∞，3）U（5，+∞）    

B . （-∞，-8）U（-5，+∞）    

C . （3，5）    

D . （-5，-3）    

5. （4分） 已知=（1，0），=（-2，2），则2-=（ ）

A . （4，2）    

B . （0，2）    

C . （4，-2）    

D . （-4.2）    

6. （4分）某校共有30个班，每个班的同学从1至45排学号，为了抽查学生体质达标情况，要求每班学号为9的同学进行交流体质检测，这里运用的抽样方法是（ ）

A . 系统抽样    

B . 分层抽样    

C . 抽签抽样    

D . 随机抽样    

7. （4分）正方体盒子中有4个白球和3个红球，从中摸出一个球，该球为红球的概率是（ ）

A .     

B .     

C .     

D .     

8. （4分）已知a=log30.2，b=30.2 ， c=0.23 ， 则a，b，c三者的大小关系是（ ）

A . c>b>a    

B . b>a>c    

C . a>b>c    

D . b>c>a    

9. （4分）若实数x，y满足约束条件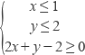： ，则z=x+y的最大值是（ ）

A . 3    

B . 1    

C . -2    

D . 2    

10. （4分）如图长方体ABCD-A1B1C1D1中，底面ABCD是边长为2的正方形，棱BB1长为 ，连接BD交AC于O，连接B1O，则B1O与底面ABC所成角的大小是（ ）

A .     

B .     

C .     

D .     

二、 填空题：本大题共5小题，每小题4分，满分20分。 (共5题；共20分)

11. （4分）已知双曲线方程为x2－2y2＝1，则它的右焦点坐标为________

12. （4分） 已知曲线 在点 处的切线与直线 垂直，则 的取值范围为________

13. （4分）复数 在复平面中所对应的点到原点的距离是________.

14. （4分）某程序框图如图所示，若输入x的值为0，则输出y的值是________ .

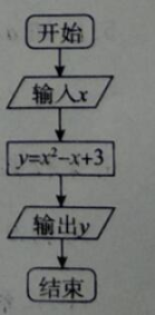
15. （4分）设m、几是两条不同的直线，α、β是两个不同的平面，给出下列四个命题：①若m∥αa，n∥a，则m∥n；②若m∥α，m∥β，则α∥β；③若m∥m，m⊥a，则n⊥a；@若m∥α，α⊥β，则m⊥β.其中正确的命题是________.

三、 解答题，本大题共5小题，满分40分，解答应写出文字说明、证明 (共5题；共40分)

16. （6分）已知椭圆 +y2=1，A，B，C，D为椭圆上四个动点，且AC，BD相交于原点O，设A（x1 ， y1），B（x2 ， y2）满足 = ．

（1） 求证： + = ；

（2） kAB+kBC的值是否为定值，若是，请求出此定值，并求出四边形ABCD面积的最大值，否则，请说明理由．

17. （8分）已知曲线 由抛物线 及抛物线 组成，直线 ： （ ）与曲线 有 （ ）个公共点.

（1） 若 ，求 的最小值；

（2） 若 ，记这 个交点为 ， ， ，其中 在第一象限， ，证明：

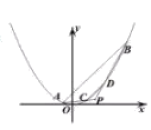
18. （8.0分）如图，己知抛物线 ，直线 交抛物线于 两点， 是抛物线外一点，连接 分别交地物线于点 ，且 .

（1） 若 ，求点 的轨迹方程.

（2） 若 ，且 平行x轴，求 面积.

19. （8分）随机抽取某农场甲、乙两块树苗试验田各10棵油茶苗，测量他们的株高（单位：cm），获得株高数据的茎叶图如图所示.

（1） 求甲试验田油茶苗株高的众数和平均值；

（2） 现从乙中这10棵油茶苗中随机抽取2棵株高不低于176cm的油茶苗，求株高178cm的油茶苗被抽中的概率。

20. （10分）某广告公司计划利用一块临街建筑物墙面设计广告宣传画，宣传画是面积为32平方米的矩形，同时要求宣传画周围要留出前后宽2米，左右宽1米的空白区域（如图），设矩形宣传画的长为x米。

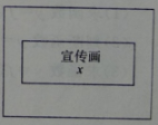
（1） 试用x表示矩形宣传画的宽；

（2） 试问当x为多少时，矩形宣传画及周围空白区域的总面积y有最小值，最小值为多少？

一、 选择题：本大题共10小题，每小题4分，满分40分 (共10题；共40分)

1-1、

2-1、

3-1、

4-1、

5-1、

6-1、

7-1、

8-1、

9-1、

10-1、

二、 填空题：本大题共5小题，每小题4分，满分20分。 (共5题；共20分)

11-1、

12-1、

13-1、

14-1、

15-1、

三、 解答题，本大题共5小题，满分40分，解答应写出文字说明、证明 (共5题；共40分)

16-1、

16-2、

17-1、

17-2、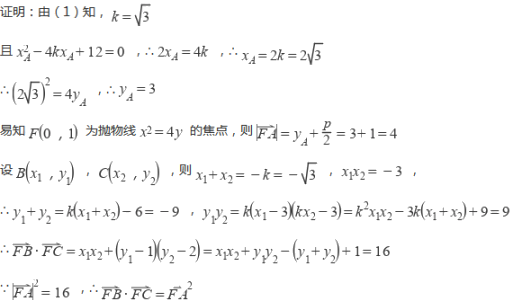

18-1、

18-2、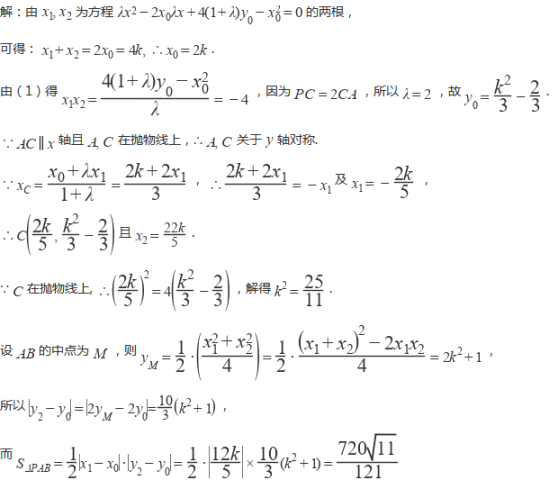

19-1、

19-2、

20-1、

20-2、