2022-2023学年重庆市高三上学期12月月考数学试题![]() 及答案
及答案
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1![]() 设
设![]() ,则( )
,则( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]()
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
【答案】C
【解析】
【分析】结合复数乘法以及复数相等的知识求得正确答案.
【详解】依题意![]() ,
,
即![]() ,
,
所以![]() ,即
,即![]() .
.
故选:C
2. 已知函数![]() ,则
,则![]() ( )
( )
A. 4 B. 6 C. 7 D. 8
【答案】D
【解析】
【分析】根据函数解析式求得正确答案.
【详解】由![]() 得
得![]() ,
,
依题意,![]() ,
,
令![]() 得
得![]() .
.
故选:D
3. 某篮球运动员练习罚篮,共20组,每组50次,每组命中球数如下表:
命中球数 | 46 | 47 | 48 | 49 | 50 |
频数 | 2 | 4 | 4 | 6 | 4 |
则这组数据的中位数和众数分别为( )
A. 48,4 B. 48.5,4 C. 48,49 D. 48.5,49
【答案】D
【解析】
【分析】根据中位数和众数的定义即可求解.
【详解】数据总个数为20个,
因此中位数是第10个与第11个数据的中位数,即![]() ,
,
众数为出现最多的数据,即数据49(出现6次),
故选:D.
4. “![]() ”是“
”是“![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】
【分析】运用诱导公式将条件化简之后,平方法可判断,注意开根号有2个解.
【详解】![]() ,
,
对上式左右平方得: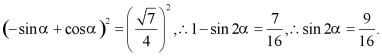
反之,当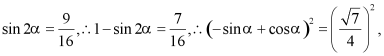
![]()
故选:A
5. 明朝朱载培发现的十二平均律,又称“十二等程律”,是世界上通用的一组音(八度)分成十二个半音音程的律制,各相邻两律之间的波长之比完全相同.若已知应钟、大吕、夹钟、仲吕的波长成等比数列,且应钟和仲吕的波长分别是![]() ,
,![]() ,则大吕和夹钟的波长之和为( )
,则大吕和夹钟的波长之和为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
【分析】等比数列第一和第四项用通项公式可求出公比,进而求出第二和第三项可得答案.
【详解】![]()

故选:C
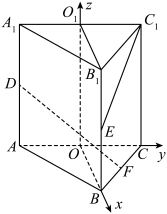
6. 如图,在直三棱柱![]() 中,
中,![]() 是等边三角形,
是等边三角形,![]() ,
,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() ,
,![]() 的中点,则异面直线
的中点,则异面直线![]() 与
与![]() 所成角的余弦值是( )
所成角的余弦值是( )
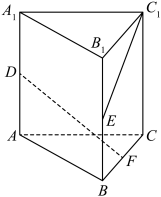
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
【分析】建立空间直角坐标系,利用向量法求得异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
【详解】设![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() ,则
,则![]() ,
,
由于![]() 是等边三角形,所以
是等边三角形,所以![]() ,
,
根据直三棱柱的性质可知,平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
由于![]() 平面
平面![]() ,所以
,所以![]() .
.
根据根据直三棱柱的性质可知,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() ,
,
由此以![]() 为原点,建立空间直角坐标系如下图所示,
为原点,建立空间直角坐标系如下图所示,
设![]() ,
,
则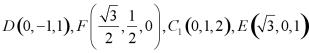 ,
,
所以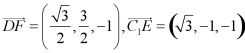 ,
,
设异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
,
则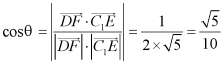 .
.
故选:A
7. 在![]() 中,
中,![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,
,![]() ,
,![]() ,
,![]() 交于点
交于点![]() ,若
,若![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
【分析】过点![]() 作
作![]() 的平行线,根据线线平行可得三角形相似,进而得到
的平行线,根据线线平行可得三角形相似,进而得到![]() 的长度之比.
的长度之比.
【详解】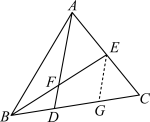
如图,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于
于![]()
在![]() 中,
中,![]() 为中位线,
为中位线,![]()
又![]()
在![]() 中,
中,![]()
所以![]()
故选:A
8. 已知函数![]() 是定义在
是定义在![]() 上的奇函数,且对任意的
上的奇函数,且对任意的![]() ,
,![]() 成立,当
成立,当![]() 时,
时,![]() ,若对任意的
,若对任意的![]() ,都有
,都有![]() ,则
,则![]() 的最大值是( )
的最大值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
【分析】求得![]() 在区间
在区间![]() 上的解析式,结合
上的解析式,结合![]() 的奇偶性画出
的奇偶性画出![]() 的图象,向左平移
的图象,向左平移![]() 个单位长度得到
个单位长度得到![]() 的图象,结合图象求得
的图象,结合图象求得![]() 的最大值.
的最大值.
【详解】当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,![]()
![]() .
.
当![]() 时,
时,![]() ,
,
![]() ,
,
此时,令![]() ,解得
,解得![]() .
.
函数![]() 是定义在
是定义在![]() 上的奇函数,图象关于原点对称;
上的奇函数,图象关于原点对称;
设![]() ,则
,则![]() ,
,
所以![]() 是偶函数,图象关于
是偶函数,图象关于![]() 轴对称,
轴对称,
由此画出![]() 的图象如下图所示:
的图象如下图所示:
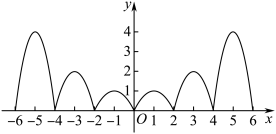
由![]() 的图象向左平移
的图象向左平移![]() 个单位得到
个单位得到![]() 的图象,如下图所示,
的图象,如下图所示,
其中![]() ,
,
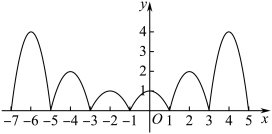
由于对任意的![]() ,都有
,都有![]() ,所以
,所以![]() 的最大值是
的最大值是![]() .
.
故选:A
【点睛】本题利用数形结合的思想方法求解含有绝对值的不等式,关键点有:由函数![]() 的函数关系式求得
的函数关系式求得![]() 的解析式、由
的解析式、由![]() 的奇偶性以及
的奇偶性以及![]() 的奇偶性画出
的奇偶性画出![]() 图象、根据图象变换的知识画出
图象、根据图象变换的知识画出![]() 的图象,结合图象求得所需要的
的图象,结合图象求得所需要的![]() 的最大值.
的最大值.
二、多选题:本题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 已知集合![]() ,
,![]() ,若
,若![]() ,则
,则![]() 的取值可以是( )
的取值可以是( )
A. 2 B. 1 C. 0 D. ![]()
【答案】ACD
【解析】
【分析】对集合B中的![]() 分类讨论即可求解.
分类讨论即可求解.
【详解】![]()
![]() 当
当![]() 时
时![]()
![]() , 显然满足条件;
, 显然满足条件;
当![]() 时,
时, ![]() , 集合
, 集合![]() ,
,
故![]() , 或
, 或![]() , 解
, 解![]() ,
,
故实数![]() 的取值的集合是
的取值的集合是 ![]() .
.
故选:ACD.
10. 《九章算术》中将底面为矩形且有一条侧棱与底面垂直的四棱锥称为阳马.已知四棱锥![]()
![]() 为阳马,底面
为阳马,底面![]() 是边长为2的正方形,其中两条侧棱长都为3,则( )
是边长为2的正方形,其中两条侧棱长都为3,则( )
A. 该阳马的体积为![]() B. 该阳马的表面积为
B. 该阳马的表面积为![]()
C. 该阳马外接球的半径为![]() D. 该阳马内切球的半径为
D. 该阳马内切球的半径为![]()
【答案】ABD
【解析】
【分析】根据相等的两条棱,求出四棱锥的高,可得其体积和表面积;然后再分析发现其外接球球心为![]() 中点,内切球的大圆半径其实是
中点,内切球的大圆半径其实是![]() 的内切圆半径.
的内切圆半径.
【详解】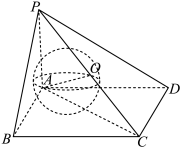
如图,不妨![]() 底面
底面![]() ,
,![]() 两两互相垂直,
两两互相垂直,
![]() 平面
平面![]()
![]() 平面
平面![]() ,又
,又![]()
![]()
由对称性:![]() ,
,
所以![]() A对;
A对;
![]() B对;
B对;
![]() 都是以
都是以![]() 为斜边的直角三角形,所以
为斜边的直角三角形,所以![]() 都在以
都在以![]() 为直径的球上,
为直径的球上,![]() C错;
C错;
分析易知:内切球的大圆半径其实是![]() 的内切圆半径,根据内切圆半径公式可得:
的内切圆半径,根据内切圆半径公式可得:
![]() D对;
D对;
故选:ABD
【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.
11. 已知定义在![]() 上的函数
上的函数![]() 的导数为
的导数为![]() ,对任意的
,对任意的![]() 满足
满足![]() ,则( )
,则( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】ABC
【解析】
【分析】构造函数![]() ,结合导数,利用已知条件求得
,结合导数,利用已知条件求得![]() 的单调性,从而确定正确答案.
的单调性,从而确定正确答案.
【详解】构造函数![]() ,
,![]() ,
,
所以![]() 在
在![]() 上递增,
上递增,
所以![]() ,
,
由![]() ,得
,得![]() ,D选项错误.
,D选项错误.
由![]() ,得
,得![]() ,C选项正确.
,C选项正确.
由![]() ,得
,得![]() ,B选项正确.
,B选项正确.
由![]() ,得
,得![]() ,A选项正确.
,A选项正确.
故选:ABC
12. 已知函数![]() 在
在![]() 上恰有3个零点,则( )
上恰有3个零点,则( )
A. ![]()
B. ![]() 在
在![]() 上单调递减
上单调递减
C. 函数![]() 在
在![]() 上最多有3个零点
上最多有3个零点
D. ![]() 在
在![]() 上恰有2个极值点
上恰有2个极值点
【答案】BC
【解析】
【分析】首先利用辅助角公式得![]() ,根据
,根据![]() 范围得到
范围得到![]() 的范围,结合图像列出不等式,则得到
的范围,结合图像列出不等式,则得到![]() 的范围,利用代入检验法即可判断B选项,对C选项证明
的范围,利用代入检验法即可判断B选项,对C选项证明![]() 达不到四个零点,再列举三个零点的情况即可,对D选项,找到一个
达不到四个零点,再列举三个零点的情况即可,对D选项,找到一个![]() 值满足3个极值点即可.
值满足3个极值点即可.
【详解】![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,
![]() 函数
函数![]() 在
在![]() 上恰有3个零点,
上恰有3个零点,
故![]() ,解得
,解得![]() ,故A错误,
,故A错误,
当![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
而正弦函数![]() 在
在![]() 上单调递减,
上单调递减,
故函数![]() 在
在![]() 上单调递减正确,故B正确,
上单调递减正确,故B正确,
令![]() ,即
,即![]() ,解得
,解得![]()
![]() ,
,![]() ,
,![]() ,
,
区间长度为![]() ,若
,若![]() 在某闭区间上有四个解,
在某闭区间上有四个解,
则区间长度至少为![]() ,比如
,比如![]() ,则
,则![]() 不可能存在四个解,
不可能存在四个解,
当![]() 时,即
时,即![]() ,
,![]() ,
,
则![]() 或
或![]() 或
或![]() ,解得
,解得![]() 或
或![]() 或
或![]() ,
,
故最多有3个零点,故C正确.
当![]() 时,此时
时,此时![]() ,令
,令![]() ,
,![]() ,
,
解得![]() ,
,![]() ,则
,则 ![]() ,
,
解得![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
此时![]() 在
在![]() 上有3个极值点,故D错误,
上有3个极值点,故D错误,
故选:BC.
【点睛】关键点睛:首先利用辅助角公式将函数化成关于正弦的函数,然后整体法结合图像得到关于![]() 的不等式,即可求出其范围,单调性问题可以通过代入检验,零点个数和极值点个数问题,通过寻找特例去证明或反驳,这也是选择题常用的方法.
的不等式,即可求出其范围,单调性问题可以通过代入检验,零点个数和极值点个数问题,通过寻找特例去证明或反驳,这也是选择题常用的方法.
三、填空题:本题共4小题,每小题5分,共20分,把答案填在答题卡的相应位置.
13. 写出一个同时满足下列条件①②的圆的标准方程:______.
①圆心在直线![]() 上,②与
上,②与![]() 轴相切.
轴相切.
【答案】![]() (答案不唯一)
(答案不唯一)
【解析】
【分析】根据给定条件,在给定直线上取点![]() ,再求出该点到y轴距离即可作答.
,再求出该点到y轴距离即可作答.
【详解】因圆心在直线![]() 上,则在直线
上,则在直线![]() 取点
取点![]() 作圆心,又该圆与
作圆心,又该圆与![]() 轴相切,则圆半径为2,
轴相切,则圆半径为2,
所以满足条件的圆的标准方程为:![]() .
.
故答案为:![]()
14. 已知![]() ,则
,则![]() 的最小值是______.
的最小值是______.
【答案】![]()
【解析】
【分析】利用基本不等式求得正确答案.
【详解】由于![]() ,
,![]() ,所以
,所以![]() ,
,
![]()
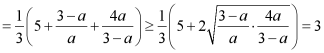 ,
,
当且仅当![]() 时等号成立.
时等号成立.
故答案为:![]()
15. 盲盒是指消费者不能提前得知具体产品款式的商品盒子.已知某盲盒产品共有3种玩偶,小明购买4个盲盒,则他能集齐3种玩偶的概率是______.
【答案】![]()
【解析】
【分析】根据给定条件,求出买4个盲盒的基本事件数,再求出集齐3种玩偶的基本事件数即可计算作答.
【详解】小明购买4个盲盒的试验有![]() 个基本事件,它们等可能,
个基本事件,它们等可能,
能集齐3种玩偶的事件A含有的基本事件数为:![]() ,
,
所以能集齐3种玩偶的概率是![]() .
.
故答案为:![]()
16. 已知函数![]() ,则曲线
,则曲线![]() 经过点
经过点![]() 的切线方程是______.
的切线方程是______.
【答案】![]() 或
或![]() .
.
【解析】
【分析】设切点,然后求导函数,进而得到该点处的切线方程,再代入点![]() 即可.
即可.
【详解】设切点为![]() 对
对![]() 求导得:
求导得:
![]() ,
,
![]() 切线方程为:
切线方程为:![]() ,
,
切线过![]() ,
,![]()
解之:![]() 或1,所以斜率
或1,所以斜率![]() 或
或![]() ,
,
又过![]() ,
,
代入点斜式得切线方程为:![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 在![]() 中,角
中,角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,
,![]() 的面积是
的面积是![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]()
(2)![]()
【解析】
【分析】(1)利用正弦定理、两角和的正弦公式、诱导公式等知识化简已知条件,从而求得![]() 的值.
的值.
(2)先求得![]() ,利用三角形
,利用三角形![]() 面积公式求得
面积公式求得![]() ,再利用余弦定理求得
,再利用余弦定理求得![]() .
.
【小问1详解】
依题意,![]() ,
,
由正弦定理得![]() ,
,
![]() ,
,
所以![]()
![]()
![]() ,由于
,由于![]() ,所以
,所以![]() ,
,
所以![]() ,则
,则![]() .
.
【小问2详解】
由(1)得![]() ,所以
,所以![]() ,
,
由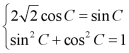 解得
解得![]() ,
,
由于![]() ,所以
,所以![]() ,
,
由余弦定理得![]() .
.
18. 如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿边
沿边![]() 翻折,使点
翻折,使点![]() 翻折到
翻折到![]() 点,且
点,且![]() .
.

(1)证明:![]() 平面
平面![]() .
.
(2)若![]() 为线段
为线段![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析
(2)![]()
【解析】
【分析】(1)利用线面垂直判定定理去证明![]() 平面
平面![]() ;
;
(2)建立空间直角坐标系,利用向量法去求二面角![]() 的余弦值.
的余弦值.
【小问1详解】
等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
则![]()
则![]() ,∴
,∴![]()
又由![]() ,可知
,可知![]()
又![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]()
故![]() 面
面![]()
【小问2详解】
过点C作![]() 平面
平面![]() ,以C为原点,分别以
,以C为原点,分别以![]()
所在直线为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系
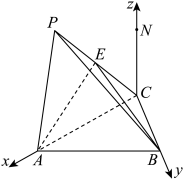
则![]() ,
,![]() ,
,![]() ,
,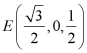 ,
,
则![]() ,
,![]()
设面![]() 法向量为
法向量为![]()
则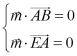 ,则
,则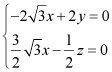 ,
,
令![]() ,则
,则![]() ,
,![]() ,则
,则![]()
又面![]() 一个法向量为
一个法向量为![]()
![]()
故二面角![]() 的余弦值为
的余弦值为![]()
19. 现在养宠物已经成为一件再正常不过的事情了,尤其是对某些人来说,养宠物是他们生活中非常重要的一件事情,他们还将自己的宠物当成是家人.某机构随机抽取了100名养宠物的人,对他们养宠物的原因进行了调查,根据调查结果,得到如下表数据:
喜欢 | 其他 | 合计 | |
男 | 10 | 20 | 30 |
女 | 40 | 30 | 70 |
合计 | 50 | 50 | 100 |
(1)根据表中调查数据,并依据![]() 的独立性检验,能否认为是否是因为喜欢宠物而养宠物与性别有关?
的独立性检验,能否认为是否是因为喜欢宠物而养宠物与性别有关?
(2)若从这100人中,按性别采用分层抽样的方法抽取10人,再从这10人中随机抽取4人,记抽到的男性人数为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
参考公式: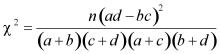 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【答案】(1)依据![]() 的独立性检验,可以认为因为喜欢宠物而养宠物与性别有关.
的独立性检验,可以认为因为喜欢宠物而养宠物与性别有关.
(2)分布列见解析;期望为![]()
【解析】
【分析】(1)计算![]() 的值,从而作出判断.
的值,从而作出判断.
(2)先求得抽取的![]() 人中,男性、女性的人数,然后按照超几何分布的分布列的计算公式,计算出分布列并求得数学期望.
人中,男性、女性的人数,然后按照超几何分布的分布列的计算公式,计算出分布列并求得数学期望.
【小问1详解】
![]() ,
,
所以,依据![]() 的独立性检验,可以认为因为喜欢宠物而养宠物与性别有关.
的独立性检验,可以认为因为喜欢宠物而养宠物与性别有关.
【小问2详解】
男性与女性人数的比例为![]() ,
,
所以抽取的![]() 人中,男性有
人中,男性有![]() 人,女性有
人,女性有![]() 人.
人.
![]() 可取0,1,2,3,
可取0,1,2,3,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]()
![]()
20. 数列![]() 满足
满足![]() ,
,![]() .
.
(1)证明:数列![]() 为等差数列.
为等差数列.
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)见解析 (2)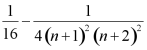
【解析】
【分析】(1)根据已知证明![]() 等于一个定值即可;
等于一个定值即可;
(2)利用裂项相消法求解即可.
【小问1详解】
证明:因为![]() ,
,
所以![]() ,又
,又![]() ,
,
所以数列![]() 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;
【小问2详解】
解:由(1)得![]() ,
,
 ,
,
则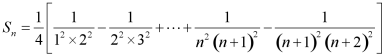
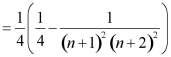
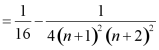 .
.
21. 已知函数![]() .
.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)若![]() ,讨论函数
,讨论函数![]() 的零点个数.
的零点个数.
【答案】(1)![]() ,
,![]()
(2)答案详见解析
【解析】
【分析】(1)利用三角恒等变换的知识化简![]() 的解析式,利用整体代入求得
的解析式,利用整体代入求得![]() 的单调递增区间.
的单调递增区间.
(2)先求得![]() 在区间
在区间![]() 上的值域,利用换元法,结合对
上的值域,利用换元法,结合对![]() 分类讨论来求得
分类讨论来求得![]() 零点的个数.
零点的个数.
![]() 小问1详解】
小问1详解】
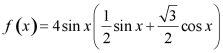
![]()
![]()
![]() ,
,
由![]() ,
,![]() ,
,
解得![]() ,
,![]() ,
,
故![]() 递增区间为
递增区间为![]() ,
,![]() .
.
【小问2详解】
![]() ,则
,则![]() ,则
,则![]() ,
,
所以![]() ,
,
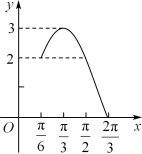
画出![]() 在区间
在区间![]() 上的图象如下图所示,
上的图象如下图所示,
令![]() ,则
,则![]() ,
,![]() ,
,
由![]() ,结合
,结合![]() 图象得:
图象得:
①当![]() 时,
时,![]() ,
,![]() ,即
,即![]() ,此时零点唯一;
,此时零点唯一;
②当![]() 时,
时,![]() 或
或![]() 或
或![]() ,此时三个零点;
,此时三个零点;
③当![]() 时,
时,![]() 或
或![]()
![]() 或
或![]() ,此时两个零点;
,此时两个零点;
④当![]() 时,
时,![]() 或
或![]()
![]()
![]() 或
或![]() (无解),此时只有一个零点;
(无解),此时只有一个零点;
⑤当![]() 时,
时,![]() 或
或![]()
![]()
![]() 或
或![]() ,此时两个零点;
,此时两个零点;
⑥当![]() ,
,![]() 时,
时,![]() 或
或![]()
![]()
![]() 或
或![]() ,此时有两个零点;
,此时有两个零点;
⑦当![]() 时,
时,![]() 或
或![]()
![]()
![]() 或
或![]() (无解),此时有一个零点;
(无解),此时有一个零点;
综上所述:当![]() 时,只有一个零点;
时,只有一个零点;
![]() 时,只有两个零点;
时,只有两个零点;![]() ,有三个零点.
,有三个零点.
22. 已知函数![]() ,
,![]() 是
是![]() 的导函数.
的导函数.
(1)若关于![]() 的方程
的方程![]() 有两个不同的正实根,求
有两个不同的正实根,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.(参考数据:
的取值范围.(参考数据:![]() )
)
【答案】(1)![]()
(2)![]()
【解析】
【分析】(1)求导,关于![]() 的方程
的方程![]() 有两个不同的正实根,即方程
有两个不同的正实根,即方程![]() 有两个不同的正实根,令
有两个不同的正实根,令![]() ,利用导数求出其单调区间,从而可得出答案;
,利用导数求出其单调区间,从而可得出答案;
(2)当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 恒成立,即
恒成立,即![]() 恒成立,令
恒成立,令![]() ,利用导数求出函数
,利用导数求出函数![]() 的最小值即可得解.
的最小值即可得解.
【小问1详解】
解:![]() ,
,
关于![]() 的方程
的方程![]() 有两个不同的正实根,
有两个不同的正实根,
即方程![]() 有两个不同的正实根,
有两个不同的正实根,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上递减,
上递减,![]() 上递增,
上递增,
所以![]() ,
,
又当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ;
;
【小问2详解】
解:当![]() 时,
时,![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
令![]() ,
,
则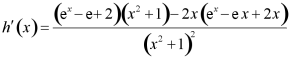

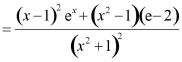 ,
,
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上递增,
上递增,
当![]() 时,
时,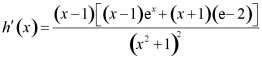
令![]() ,
,
则![]() ,
,
所以函数![]() 在
在![]() 上递增,
上递增,
所以![]() ,
,
所以当![]() 时,
时,![]() ,即
,即![]() ,
,
所以函数![]() 在
在![]() 上递增,
上递增,
所以![]() ,
,
所以![]() ,
,
所以![]() .
.
【点睛】本题考查了利用导数研究方程的根及函数不等式恒成立问题,解决两个问题的关键都是分离参数,计算量较大,有一定的难度.