2022-2023年重庆高一数学上学期期末试卷及答案

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 化成弧度为( )

A. B. C. D.

【答案】A

2. 已知集合，，则( )

A. B. C. D.

【答案】B

3. 已知：正整数能被6整除，，则是的( )

A. 充分不必要条件 B. 必要不充分条件

C. 充要条件 D. 既不充分也不必要条件

【答案】A

4. 已知，，，则( )

A. B. C. D.

【答案】A

5. 命题，使得函数在上不单调，则命题的否定是( )

A. ，函数在上不单调

B. ，函数在上单调

C. ，函数在上单调

D. ，函数在上单调

【答案】B

6. 下列函数中既是奇函数又是减函数的是( )

A. B.

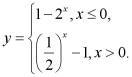C. D.

【答案】C

7. 已知函数，，，则的取值范围是( )

A. B. C. D.

【答案】C

8. 已知函数，若，则实数的取值范围是( )

A. B.

C. D.

【答案】B

二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.

9. 下列说法中正确的是( )

A. 任何集合都至少有两个子集

B. 设为全集，，，是的子集，若，则

C. 命题“，”的否定为“，”

D. 若是的必要不充分条件，的必要不充分条件是，则是的充分条件

【答案】BD

10. 已知幂函数，则( )

A. ，函数的图像与坐标轴没有交点

B. ，使得是奇函数

C. 当时，函数在上单调递增

D. 当时，函数的值域为

【答案】BCD

11. 已知，则( )

A. B. C. D.

【答案】AB

12. 已知函数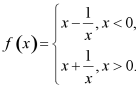和函数，关于的方程有个实根，则下列说法中正确的是( )

A. 当时， B. 当时，

C. ， D. ，

【答案】BC

三、填空题：本题共4小题，每小题5分，共20分.

13. 函数的定义域是______.

【答案】

14. ______.

【答案】##

15. 已知某扇形材料的面积为，圆心角为，则用此材料切割出的面积最大的圆的周长为______.

【答案】

16. 已知函数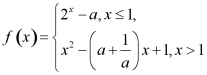.若，则的值域是______；若恰有2个零点，则实数的取值范围是______.

【答案】 ①. ②.

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

17. 已知，集合，.

(1)当时，求，；

(2)若，求的取值范围.

【答案】(1)，

(2)

18. (1)求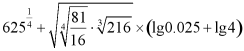的值；

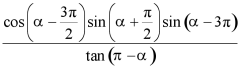(2)已知，求的值.

【答案】(1)2；(2)

19. 已知，.

(1)求的取值范围；

(2)求的最小值.

【答案】(1)

(2)

20. 已知，集合，.

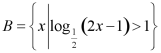(1)求集合；

(2)若，求实数的取值范围.

【答案】(1)

(2)

21. 某电影院每天最多可制作500桶爆米花，每桶售价相同，根据影院的经营经验，当每桶售价不超过20元时，当天可售出500桶；当每桶售价高于20元时，售价每高出1元，当天就少售出20桶.已知每桶爆米花的成本是4元，设每桶爆米花的售价为(且)元，该电影院一天出售爆米花所获利润为元.(总收入=总成本+利润)

(1)求关于的函数表达式；

(2)试问每桶爆米花的售价定为多少元时，该电影院一天出售爆米花所获利润最大？最大利润为多少元？

【答案】(1)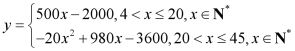

(2)当或25时，利润最多为8400元

22. 已知函数的定义域为，且.

(1)求，判断并证明其单调性；

(2)求方程的根；

(3)若不等式对任意恒成立，求实数的取值范围.

【答案】(1)，在上单调递增，证明见解析

(2)

(3)