2012年青海普通高中会考数学真题及答案
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.满分100分考试时间90分钟.
第Ⅰ卷（选择题共60分）
一.选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，有且只有一项是符合题目要求的）
1.sin150°的值等于
A.
B.
C.
D.
2.若A={0,1,2,3},B={0,3,6,9},则A∩B=
A.{1,2}B.{0,1}C.{0,3}D.{3}
3.下列函数中，既是奇函数，又是增函数的是
A.
B.
（
＞0）C.
D.
4.方程
有实数解的一个区间是
A.(-2，-1)B.(-1,0)C.(1,2)D.(0,1)
5.过点（1,0）且与直线
平行的直线方程是
A.
B.
C.
D.
6.已知向量a=（3,1），b=（-1,3），那么
A.a⊥bB.a∥bC.a＞bD.
a
＞
b
7.一个年级有16个班级，每个班级有50名学生，把每个班级的学生都从1到50编排.为了交流学习经验，要求每班编号为14的学生留下进行交流，这里运用的是
A.分层抽样B.抽签法C.随机数表法D.系统抽样
8.不等式
＞0的解集是
A.（
，1）B.（
）∪（
）C.（
）D.（
）∪（
）
9.设长方体的长、宽、高分别为
、
、
，其顶点都在球面上，则该球的表面积为
A.
B.
C.
D.
10.在正方体ABCD—A1B1C1D1中，BC1与AC所成的角为
A.30°B.45°C.60°D.90°
11.设{
}为等差数列，公差
=
，
为其前
项和，若
，则
=
A.24B.22 C.20D.18
12.若cos
=
，
是第三象限的角，则sin（
）=
A.
B.
C.
D.
第Ⅱ卷（非选择题共60分）
二.填空题（本大题有4个小题，每小题5分，共20分）
13.在△ABC中，若
=5，∠B=
，sinA=
，则
=.
14.圆心在原点且与直线
相切的圆的方程为.
15.某班委会由4名男生和3名女生组成.现从中选出2人担任正副班长，其中至少有1名女生当选的概率是.
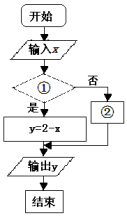
16.已知函数
，右图表示的是给出
的值，
求其对应的函数值
的程序框图，①处填写；②处填写.
三.解答题（本大题有4个小题，每小题10分，共40分.解答应写出文字说明、证明过程或演算步骤）
17.函数
（
＞0，且
≠1）的图象过点（
）.
（1）求
的值；
（2）求函数的定义域.
18.已知函数
（1）求函数
的最小正周期；
（2）求函数
的最大值及取得最大值时
的值.
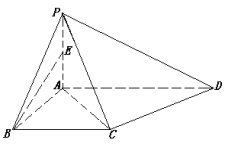19.如图，在四棱锥P—ABCD中，∠DAB=∠ABC=90°，PA⊥平面ABCD，点E是PA的中点，AB=BC=1，AD=2.
求证：（1）平面PCD⊥平面PAC;
（2）BE∥平面PCD.
20.等比数列{
}的前
项和为
，已知
、
、
成等差数列.求
（1）数列{
}的公比
；
（2）若
，求
.
数学参考答案及评分
一.选择题：ACADAADBBCCD
二.填空题：13.
14.
15.
16.
＜2，
三.解答题：（对于不同的解法，可参照评分意见相应步骤给分）
17.解：（1）将（-1,0）代入
中，有
---------------------2分
则
，∴
----------------------------4分
（2）由（1）知
，
＞0，∴
＞
----------------------------7分
∴函数的定义域为{
＞
} ----------------------------9分
18.解：（1）
----------------------------3分
最小正周期为
----------------------------5分
（2）
，即
，(
∈
)
得
(
∈
) ----------------------------7分
∴当
(
∈
)时，函数有最大值，
最大值为
----------------------------9分
19.证明（1）过点C作CH⊥AD，垂足为点H，则DH=CH=1，CD=
又∵AC=
,AD=2，∴∠ACD=90°，∴CD⊥AC----------------------------2分
又∵PA⊥CD,CD⊥平面PAC
∵CD
平面PCD∴平面PCD⊥平面PAC ----------------------------5分
（2）取PD的中点F，连结EF、CF，则,EF
BC.
∴四边形BEFC为平行四边形，∴BE∥CF
∵CF
平面PCD，∴BE∥平面PCD. ----------------------------9分
20.解：（1）依题意有
-------------2分
∵
≠0，
≠0∴
----------------------------4分
（2）由已知可得：
∴
----------------------------6分
∴
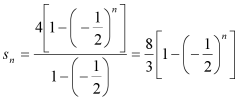
----------------------------9分