2020-2021年北京市朝阳区高二数学上学期期末试题及答案
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,选出符合题目要求的一项.
1. 圆![]() 的圆心C的坐标为( )
的圆心C的坐标为( )
A. (1,0) B. (-1,0) C. (2,0) D. (-2,0)
【答案】B
2. 已知直线l的方向向量为![]() ,平面α的法向量为
,平面α的法向量为![]() ,若
,若![]() ,
,![]() ,则直线l与平面α( )
,则直线l与平面α( )
A. 垂直 B. 平行
C. 相交但不垂直 D. 位置关系无法确定
【答案】A
3. 双曲线![]() 的焦点到渐近线的距离为( )
的焦点到渐近线的距离为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
4. 如图,已知直线l与圆![]() 相交于A,B两点,若平面向量
相交于A,B两点,若平面向量![]() ,
,![]() 满足
满足![]() ,则
,则![]() 和
和![]() 的夹角为( )
的夹角为( )
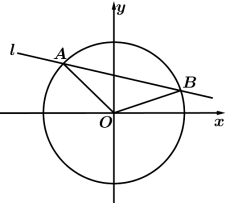
A. 45° B. 90° C. 120° D. 150°
【答案】C
5. 光圈是一个用来控制光线透过镜头,进入机身内感光面的光量的装置.表达光圈的大小我们可以用光圈的F值表示,光圈的F值系列如下:F1,F1.4,F2,F2.8,F4,F5.6,F8,…,F64.光圈的F值越小,表示在同一单位时间内进光量越多,而且上一级的进光量是下一级的2倍,如光圈从F8调整到F5.6,进光量是原来的2倍.若光圈从F4调整到F1.4,则单位时间内的进光量为原来的( )
A. 2倍 B. 4倍 C. 8倍 D. 16倍
【答案】C
6. 过抛物线![]() 上的一点
上的一点![]() 作其准线的垂线,垂足为
作其准线的垂线,垂足为![]() ,抛物线的焦点为
,抛物线的焦点为![]() ,直线
,直线![]() 在
在![]() 轴下方交抛物线于点
轴下方交抛物线于点![]() ,则
,则![]() ( )
( )
A. 1 B. ![]() C. 3 D. 4
C. 3 D. 4
【答案】D
7. 下列有四个说法:
①若直线与抛物线相切,则直线与抛物线有且只有一个公共点:
②函数![]() 在定义域上单调递减;
在定义域上单调递减;
③某质点沿直线运动,位移![]() (单位:m)与时间t(单位:s)满足关系式
(单位:m)与时间t(单位:s)满足关系式![]() 则
则![]() 时的瞬时速度是10 m/s;
时的瞬时速度是10 m/s;
④设x>0,![]() ,
,![]() ,则在(0,+∞)上函数
,则在(0,+∞)上函数![]() 的图象比
的图象比![]() 的图象要“陡峭”.
的图象要“陡峭”.
其中正确的序号是( )
A. ①③ B. ②③ C. ①④ D. ③④
【答案】A
8. 如图,将边长为4的正方形折成一个正四棱柱的侧面,则异面直线AK和LM所成角的大小为( )
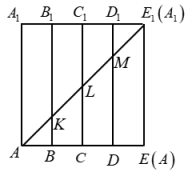
A. 30° B. 45° C. 60° D. 90°
【答案】D
9. 已知椭圆![]() :
:![]() ,椭圆的左、右焦点分别为
,椭圆的左、右焦点分别为![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上的任意一点,且满足
上的任意一点,且满足![]() ,则椭圆离心率的取值范围是( )
,则椭圆离心率的取值范围是( )
A. ![]() B.
B. 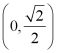 C.
C. 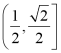 D.
D. 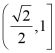
【答案】B
10. 如图,在三棱锥O-ABC中,三条侧棱OA,OB,OC两两垂直,且OA,OB,OC的长分别为a,b,c. M为△ABC内部及其边界上的任意一点,点M到平面OBC,平面OAC,平面OAB的距离分别为a0,b0,c0,则![]() ( )
( )
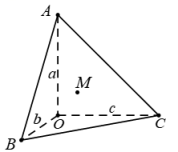
A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
【答案】C
二、填空题:本大题共6小题每小题5分,共30分.把答案填在答题卡上.
11. 只知两条直线![]() ,
,![]() 平行,则m的值为______.
平行,则m的值为______.
【答案】4
解:两条直线![]() ,
,![]() 平行,则
平行,则![]() ,得
,得![]() ,
,
12. 等差数列![]() 满足
满足![]() ,
,![]() ,则
,则![]() _________.
_________.
【答案】![]()
解:等差数列![]() 满足
满足![]() ,
,![]() ,设公差为
,设公差为![]() ,则
,则![]() ,
,
则![]() ,
,
13. 已知函数![]() (a∈R),且
(a∈R),且![]() ,则a的值为_________.
,则a的值为_________.
【答案】1
解:对函数求导得![]() ,
,
则![]() ,得
,得![]() .
.
14. 如图,平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°.CD=CC1=1.则A1C与平面C1BD_______(填“垂直”或“不垂直”);A1C的长为_______.
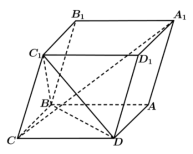
【答案】 ①. 垂直 ②. ![]()
解:设![]() ,
,![]() ,
,![]() ,由题意可得
,由题意可得![]() ,
,
则![]()
![]() ,
,![]() ,同理可证
,同理可证![]() ,
,
![]() ,故
,故![]() 平面
平面![]() .
.
![]() ∠C1CB=∠C1CD=∠BCD=60°.CD=CC1=1,
∠C1CB=∠C1CD=∠BCD=60°.CD=CC1=1,
![]() ,
,
![]()
![]() ,
,
即A1C的长为![]() .
.
故答案![]() :垂直;
:垂直;![]()
15. 2020年11月24日我国在中国文昌航天发射场,用长征五号遥五运载火箭成功发射探月工程“嫦娥五号”探测器,开启我国首次地外天体采样返回之旅.2004年,中国正式开展月球探测工程,并命名为“嫦娥工程”.2007年10月24日“嫦娥一号”成功发射升空,探月卫星运行到地月转移轨道之前在以地心![]() 为椭圆焦点的Ⅰ、Ⅱ、Ⅲ三个轨道飞行(如图所示),三个椭圆轨道的长半轴长、半焦距和离心率分别为
为椭圆焦点的Ⅰ、Ⅱ、Ⅲ三个轨道飞行(如图所示),三个椭圆轨道的长半轴长、半焦距和离心率分别为![]() ,探月卫星沿三个椭圆轨道的飞行周期(环绕轨道一周的时间)分别为16小时,24小时和48小时,已知对于同一个中心天体的卫星,它们运动周期的平方与长半轴长的三次方之比是定值.现有以下命题:①
,探月卫星沿三个椭圆轨道的飞行周期(环绕轨道一周的时间)分别为16小时,24小时和48小时,已知对于同一个中心天体的卫星,它们运动周期的平方与长半轴长的三次方之比是定值.现有以下命题:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .则以上命题为真命题的是___________.(写出所有真命题的序号)
.则以上命题为真命题的是___________.(写出所有真命题的序号)
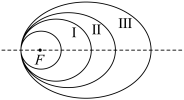
【答案】①③④
解:由题意知:三个椭圆轨道的近地点相同且都以地心![]() 为焦点,
为焦点,
∴![]() ,故①正确,
,故①正确,
![]() ,即
,即![]() ,则
,则![]() 且
且![]() ,故②错误,③正确,
,故②错误,③正确,
∵若地球半径为![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,![]() ,故
,故![]() ,
,
由上知:![]() ,所以
,所以![]() ,故④正确.
,故④正确.
故答案为:①③④
16. 把正奇数列按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,则在第n(n∈N*)组里有________个数;第9组中的所有数之和为________.
【答案】 ①. ![]() ②. 2465
②. 2465
解:第1组有1个数,
第2组有3个数,
第3组有5个数,
……
第n组有![]() 个数.
个数.
前8组的数字个数分别为1,3……15,共64项,第9组中的数字个数有2×9-1=17个,
设把正奇数列的前n项和为![]() ,则第9组中的所有数之和:
,则第9组中的所有数之和:
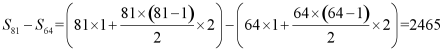 .
.
故答案为:![]() ;2465.
;2465.
三、解答题:本大题共5小题,共70分.解答应写出文字说明,演算步骤或证朋过程.
17. 已知函数![]()
(1)求曲线![]() 在点(e,
在点(e,![]() )的切线方程;
)的切线方程;
(2)求函数![]() 的单调区间.
的单调区间.
【答案】(1)![]() ; (2)在
; (2)在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
解:(1)由![]() 得
得![]() ,
,
所以切线斜率为![]()
切点坐标为![]() ,
,
所以切线方程为![]() ,即
,即![]() ;
;
(2)![]() ,
,
令![]() ,得
,得![]() .
.
![]() 当
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
18. 已知圆![]() ,若直线
,若直线![]() 与圆C相交于A,B两点,且
与圆C相交于A,B两点,且![]() .
.
(I)求圆C的方程.
(II)请从条件①条件②这两个条件中选择一个作为点P的坐标,求过点P与圆C相切的直线l2的方程.
①(2,-3);②(1,![]() ).
).
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【答案】(I)![]() ;(II)选①:
;(II)选①:![]() 或
或![]() ;选②:
;选②:![]() .
.
解:(I)设圆心到直线![]() 的距离为
的距离为![]() ,则
,则![]() ,即
,即![]() ,
,
又![]() ,
,![]() ,
,
故圆C的方程为![]() ;
;
(II)选①:当直线![]() 斜率不存在时,
斜率不存在时,![]() 的方程为
的方程为![]() ,恰好与圆相切,满足题意;
,恰好与圆相切,满足题意;
当直线![]() 斜率存在时,设
斜率存在时,设![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
则圆心到直线![]() 的距离为
的距离为![]() ,解得
,解得![]() ,
,
此时直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
综上,直线![]() 的方程为
的方程为![]() 或
或![]() ;
;
选②,可得![]() 在圆上,即
在圆上,即![]() 为切点,
为切点,
则切点与圆心连线斜率为![]() ,则切线斜率为
,则切线斜率为![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
19. 已知![]() 是各项均为正数的等比数列,
是各项均为正数的等比数列,![]() .
.
(I)求数列{an}的通项公式;
(II)若数列{bn}的通项bn满足![]() ,求{bn}的前n项和Sn的最小值及取得最小值时n的值.
,求{bn}的前n项和Sn的最小值及取得最小值时n的值.
【答案】(I)![]() ;(II)当
;(II)当![]() 时,
时,![]() 取得最小值为
取得最小值为![]()
解:(I)设等比数列![]() 的公比为
的公比为![]() ,且
,且![]() ,
,
则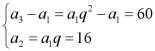 ,解得
,解得![]() ,
,
![]()
(II)![]()
![]() ,
,![]() ,
,
![]() ,
,
则当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() .
.
20. 在如图所示的多面体中,![]() 且
且![]() ,
,![]() ,
,![]() 且
且![]() ,
,![]() 且
且![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,M,N分别为棱
,M,N分别为棱![]() 的中点.
的中点.
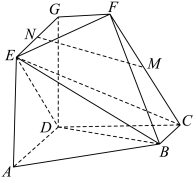
(I)求点F到直线EC的距离;
(II)求平面BED与平面EDC夹角的余弦值;
(III)在棱GF上是否存在一点Q,使得平面MNQ//平而EDC?若存在.指出点Q的位置,若不存在,说明理由.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)不存在,证明见解析;
;(III)不存在,证明见解析;
解:(I)由![]() 平面ABCD知,
平面ABCD知,![]() ,
,![]() ,又
,又![]() ,
,
则建立以D点为原点的空间直角坐标系,如图所示,

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]()
![]() ,
,![]() ,
,
所以点F到直线EC的距离为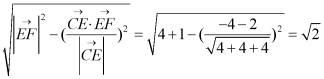
(II)由(I)知,![]() ,
,![]() ,
,![]()
设平面BED的法向量为![]() ,
,
则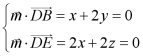 ,令
,令![]() ,则
,则![]()
设平面EDC的法向量为![]() ,
,
则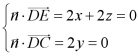 ,令
,令![]() ,则
,则![]()
故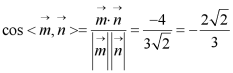
由图知,二面角![]() 为锐二面角,故余弦值为
为锐二面角,故余弦值为![]()
(III)设GF上存在一点Q,设![]() ,
,![]()
则![]() ,
,![]()
设平面MNQ的法向量为![]()
则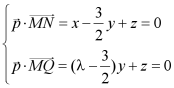 ,令
,令![]() ,则
,则![]()
若平面![]() 平面
平面![]() ,则
,则![]() ,
,
故![]() 不存在,即不存在点Q使得平面
不存在,即不存在点Q使得平面![]() 平面
平面![]()
21. 在平面直角坐标系![]() 中,点
中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() 是动点,且直线
是动点,且直线![]() 与
与![]() 的斜率之积等于
的斜率之积等于![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() 是曲线
是曲线![]() 的左焦点,过点
的左焦点,过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,过
两点,过![]() ,
,![]() 分别作直线
分别作直线![]() 的垂线与
的垂线与![]() 轴相交于
轴相交于![]() ,
,![]() 两点.若
两点.若![]() ,求此时直线
,求此时直线![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
解:(1)设![]() ,则
,则![]() ,
,
所以可得动点P的轨迹C的方程为![]()
(2)可得![]() ,设直线l的方程为
,设直线l的方程为![]() ,
,![]()
联立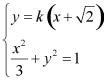 可得
可得![]()
所以![]()
因为过A,B分别作直线l的垂线与x轴相交于M,N两点
所以![]()
所以直线![]() 的方程为
的方程为![]() ,令
,令![]() 可得
可得![]() ,同理可得
,同理可得![]()
所以![]()
所以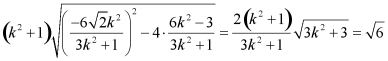
解得![]() ,所以
,所以![]()