2012年重庆普通高中会考数学真题

一. 填空题：本大题共10小题，每小题5分，共计50分。在每小题给出的四个备选选项中，只有一个是符合题目要求的

1.在等差数列中，则的前5项和=

A.7 B.15 C.20 D.25

2. 不等式的解集为

A. B. C. D.

3. 对任意的实数k，直线y=kx+1与圆 的位置关系一定是

A. 相离 B.相切 C.相交但直线不过圆心 D.相交且直线过圆心

4.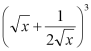的展开式中常数项为

A. B. C. D.105

5.设是议程的两个根，则的值为

（A）-3 （B）-1 （C）1 （D）3

6.设R，向量且，则

（A） （B） （C） （D）10

7.已知是定义在R上的偶函数，且以2为周期，则“为[0，1]上的增函数”是“为[3，4]上的减函数”的

（A）既不充分也不必要的条件 （B）充分而不必要的条件

（C）必要而不充分的条件 （D）充要条件

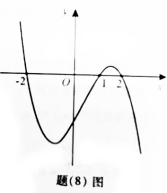
8.设函数在R上可导，其导函数为，且函数的图像如题（8）图所示，则下列结论中一定成立的是

（A）函数有极大值和极小值

（B）函数有极大值和极小值

（C）函数有极大值和极小值

（D）函数有极大值和极小值

9.设四面体的六条棱的长分别为1，1，1，1，和，且长为的棱与长为的棱异面，则的取值范围是

（A） （B） （C） （D）

10.设平面点集，则所表示的平面图形的面积为

（A） （B） （C） （D）

二 填空题：本大题共5小题，每小题5分，共25分，把答案分别填写在答题卡相应位置上

11.）若，其中为虚数单位，则 ；

12. 。

13.设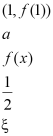的内角的对边分别为，且则

14.过抛物线的焦点作直线交抛物线于两点，若则

= 。

15.某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课个1节，则在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为 （用数字作答）.

三 解答题：本大题共6小题，共75 分，解答应写出文字说明、证明过程或演算步骤.

16. （本小题满分13分，（Ⅰ）小问6分，（Ⅱ）小问7分.）

设其中，曲线在点处的切线垂直于轴.

（Ⅰ） 求的值；

（Ⅱ） 求函数的极值.

17. （本小题满分13分，（Ⅰ）小问5分，（Ⅱ）小问8分.）

甲、乙两人轮流投篮，每人每次投一票.约定甲先投中者获胜，一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为，乙每次投篮投中的概率为，且各次投篮互不影响.

（Ⅰ） 求甲获胜的概率；

（Ⅱ） 求投篮结束时甲的投篮次数的分布列与期望

18.（本小题满分13分（Ⅰ）小问8分（Ⅱ）小问5分）

设，其中

（Ⅰ）求函数 的值域

（Ⅱ）若在区间上为增函数，求 的最大值。

19.（本小题满分12分（Ⅰ）小问4分（Ⅱ）小问8分）

如图，在直三棱柱 中，AB=4，AC=BC=3，D为AB的中点

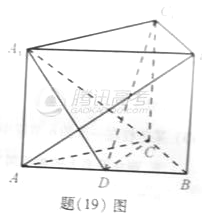（Ⅰ）求点C到平面 的距离;

（Ⅱ）若 求二面角 的平面角的余弦值。

20.（本小题满分12分（Ⅰ）小问5分（Ⅱ）小问7分）

如图，设椭圆的中心为原点O，长轴在x轴上，上顶点为A，左右焦点分别为，线段 的中点分别为，且△ 是面积为4的直角三角形。

（Ⅰ）求该椭圆的离心率和标准方程；

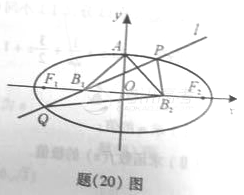（Ⅱ）过 做直线交椭圆于P，Q两点，使，求直线的方程

21.（本小题满分12分，（I）小问5分，（II）小问7分。）

设数列的前项和满足，其中。

（I）求证：是首项为1的等比数列；

（II）若，求证：，并给出等号成立的充要条件。