2022-2023年江西萍乡六年级上册期末数学试卷及答案(人教版)
一、填空题。（每空1分，共20分）
1. 
的倒数是（ ），0.35的倒数是（ ），1的倒数是（ ）。
【答案】 ①. 
②. 
③. 1
【解析】
【分析】根据倒数的意义：乘积是1的两个数互为倒数，据此解答即可。
【详解】
的倒数是
。
0.35＝
0.35的倒数是
。
1×1＝1
1的倒数是1。
【点睛】此题考查的目的是理解倒数的意义，掌握求一个数的倒数的方法。
2. 252千米的
是（ ）千米，18比（ ）多20%。
【答案】 ①. 168 ②. 15
【解析】
【分析】求252千米的
是多少千米，用252×
即可；18比要求的未知数多20%，以这个未知的数量为单位，18相当于未知量的1＋20%，用数量除以对应的分率得单位“1”量，据此解答。
【详解】252×
＝168（千米）
252千米的
是168千米；
18÷（1＋20%）
＝18÷1.2
＝15
18比15多20%。
【点睛】本题主要考查了学生分析问题解答问题的能力。
3. 
时∶25分的比值是（ ），化成最简整数比是（ ）。
【答案】 ①. 
②. 9∶5
【解析】
【分析】比的基本性质：比的前项和后项同时乘或除以相同的数（0除外），比值不变；
比的前项和后项的单位不统一，先根据进率“1时＝60分”换算单位，再化简比；利用“比的基本性质 ”把比化简成最简单的整数比；
然后根据求比值的方法，用最简比的前项除以比的后项即得比值。
【详解】
时∶25分
＝（
×60）分∶25分
＝45∶25
＝（45÷5）∶（25÷5）
＝9∶5
9∶5
＝9÷5
＝
时∶25分的比值是
，化成最简整数比是9∶5。
【点睛】掌握化简比和求比值的方法是解题的关键。注意化简比的结果是一个比，它的前项和后项都是整数，并且是互质数；求比值的结果是一个数值，可以是整数、小数或最简分数。
4. （ ）÷75＝
＝8∶（ ）＝32%＝（ ）（填小数）。
【答案】24；50；25；0.32
【解析】
【分析】百分数化成小数，小数点向左移动两位，同时去掉百分号；
小数化成分数，两位小数先化成分母为100的分数，再化简成最简分数；
分数的基本性质：分数的分子和分母同时乘或除以相同的数（0除外），分数的大小不变；
分数与除法的关系：分子相当于被除数，分母相当于除数，分数线相当于除号；
分数与比的关系：分子相当于比的前项，分母相当于比的后项，分数线相当于比号。
【详解】32%＝0.32
0.32＝
＝
＝
＝
，
＝24÷75
＝
＝
＝8∶25
即24÷75＝
＝8∶25＝32%＝0.32。
【点睛】掌握小数、分数、百分数的互化，分数的基本性质，分数与除法、比的关系是解题的关键。
5. 一个长方形的周长是60cm，长和宽之比是3∶2，这个长方形的面积是（ ）cm2。
【答案】216
【解析】
【分析】因为长方形周长＝（长＋宽）×2，所以长＋宽＝60÷2＝30（cm）又因为长与宽的比是3∶2，所以每一份的长度是30÷（3＋2）＝6（cm），那么长是6×3＝18（cm），宽是6×2＝12（cm），再根据面积＝长×宽计算即可。
【详解】长与宽的和是：60÷2＝30（cm）
长是：30÷（3＋2）×3
＝30÷5×3
＝6×3
＝18（cm）
宽是：30÷（3＋2）×2
＝30÷5×2
＝6×2
＝12（cm）
面积是：18×12＝216（cm2）
这个长方形的面积是216cm2。
【点睛】解决本题的关键是根据周长和长与宽的比求出长方形的长和宽。
6. 如下图，第6个图形一共用（ ）根小棒。
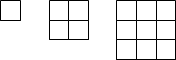
【答案】84
【解析】
【分析】根据图可知，第一个图形有4根小棒，即1×4＝1×（1＋1）×2；第二个图形有12根小棒，即2×6＝2×（2＋1）×2，第三个图形有24根小棒，即3×8＝3×（3＋1）×2，由此即可知道第n个图形中小棒的根数有：n×（n＋1）×2，据此当n＝6时，代入式子即可求出有多少根小棒。
【详解】由分析可知：第n个图形的小棒数量是：n×（n＋1）×2
即当n＝6时
6×（6＋1）×2
＝6×7×2
＝42×2
＝84（根）
所以第6个图形中一共有84根小棒。
【点睛】通过数形结合，从已知的图形或数据中找到规律，并按规律解题。
7. 如图，能画（ ）条对称轴。图中一个圆的周长是18.84dm。圆的半径是（ ）dm，圆的面积是（ ）dm2，长方形的周长是（ ）dm。
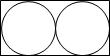
【答案】 ①. 2##二##两 ②. 3 ③. 28.26 ④. 36
【解析】
【分析】一个图形沿一条直线对折，直线两旁的图形完全重合，这样的图形叫做轴对称图形，折痕所在的直线就是对称轴。据此可得出这个图形能画两条对称轴；根据圆的周长公式：C＝
，代入数据，求出圆的半径，再利用圆的面积公式：S＝
，即可求出圆的面积，长方形的周长等于六条圆的直径。据此解答。
【详解】如图：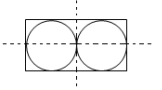
能画两条对称轴；
18.84÷2÷3.14＝3（dm）
3.14×3×3＝28.26（dm2）
2×3×6＝36（dm）
即圆的半径是3dm，圆的面积是28.26dm2，长方形的周长是36dm。
【点睛】此题主要考查轴对称图形的意义以及圆的周长和圆的面积的公式的熟练运用。
8. 六年级同学参加体能测试，有285人达标，达标率为95%，六年级有（ ）人。
【答案】300
【解析】
【分析】根据题意，六年级有285人达标，达标率为95%，即达标的285人占六年级总人数的95%，把六年级总人数看作单位“1”，根据“已知一个数的百分之几是多少，求这个数”，用达标的人数除以95%，即可求出六年级的总人数。
【详解】285÷95%
＝285÷0.95
＝300（人）
六年级有300人。
【点睛】本题考查百分率问题，理解达标率的意义，找出单位“1”，单位“1”未知，根据百分数除法的意义解答。
9. 铺一条800米的路，已经铺了440m，还剩（ ）%没有铺。
【答案】45
【解析】
【分析】用剩下没铺的长度除以总长度即可解答。
【详解】（800－440）÷800
＝360÷800
＝45%
【点睛】求一个数是另一个数的百分之几，用这个数除以另一个数即可。
10. 一只挂钟的分针长20厘米，经过15分钟后，分针的尖端所走的路程是（ ）厘米。
【答案】31.4
【解析】
【分析】经过15分钟，所形成的轨迹是一个
圆，分针的尖端所走路程是半径为20厘米的圆周长的
，根据半径求出圆的周长，然后再乘
即可。
【详解】2×3.14×20×
＝6.28×20×
＝125.6×
＝31.4（厘米）
即分针的尖端所走的路程是31.4厘米。
【点睛】明确15分钟分针的尖端所走的轨迹是解决此题的关键。
二、判断题（每空2分，共10分）
11. 一个数（0除外）除以分数，商可能比这个数小。（ ）
【答案】√
【解析】
【分析】一个数（0除外）除以小于1的数，商比原来的数大；
一个数（0除外）除以大于1的数，商比原来的数小。
【详解】如： 1÷
＝2，2＞1，商比这个数大；
1÷
＝
，
＜1，商比这个数小；
所以，一个数（0除外）除以分数，商可能比这个数小。
原题说法正确。
故答案
：√
【点睛】掌握判断商与被除数之间大小关系的方法是解题的关键。
12. 某小学六①男生人数比女生少10%，也可以说女生人数比男生多10%。（ ）
【答案】×
【解析】
【分析】把女生人数看作单位“1”，男生人数比女生少10%，则男生人数就相当于女生的l－10%＝90%，那么女生比男生多百分之几，用（1－90%）除以90%即可得解。
【详解】（1－90%）÷90%×100%
＝0.1÷0.9×100%
≈0.111×100%
＝11.1%
女生人数比男生多11.1%，原题说法错误。
故答案为：×
【点睛】解答此类问题的关键是找准单位“1”，考查了学生对分数意义的理解以及分析问题的能力。
13. 圆的直径扩大到原来的3倍,周长和面积也就扩大到原来的3倍． （ ）
【答案】×
【解析】
14. 半圆的周长是这个圆的周长的一半。（ ）
【答案】×
【解析】
【分析】封闭图形一周的长度叫做图形的周长，据此解答。
【详解】半圆的周长如下图所示：
圆的周长的一半如下图所示：
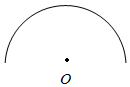
所以上面的说法错误的。
故答案
：×。
【点睛】本题主要考查周长的意义。
15. 工人叔叔植了120棵树，成活了115棵，成活率为115%。（ ）
【答案】×
【解析】
【分析】用成活棵树除以种植棵树，求出成活率，据此判断即可。
【详解】成活率：
，本题说法错误。
故答案为：×
【点睛】本题考查百分数，解答本题的关键是掌握成活率的计算方法。
三、选择题。（每题2分，共8分）
16. 一种椅子的椅面是一个圆环，内直径为2米，外直径为4米。这种椅面的面积是（ ）平方米。
A. 37.68 B. 3.14 C. 9.42
【答案】C
【解析】
【分析】根据题意可知，椅面是一个圆环，求这种椅面的面积，就是求圆环的面积。根据圆环的面积公式S环＝π（R2－r2），代入数据计算即可。
【详解】2÷2＝1（米）
4÷2＝2（米）
3.14×（22－12）
＝3.14×（4－1）
＝3.14×3
＝9.42（平方米）
这种椅面的面积是9.42平方米。
故答案为：C
【点睛】本题考查圆环面积公式的灵活运用。
17. 体育馆在图书馆的南偏西38°方向700米处，则图书馆在体育馆的（ ）。
A. 西偏南38°方向700米处 B. 北偏东38°方向700米处 C. 北偏东52°方向700米处
【答案】B
【解析】
【分析】根据“上北下南，左西右东”确定方向，以图书馆为观测点时，体育馆在图书馆正南方向偏西38°方向上，如果以体育馆为观测点，那么图书馆在体育馆正北方向偏东38°或正东方向偏北52°方向上，两地之间的距离不变，据此解答。
【详解】
如图所示，体育馆在图书馆的南偏西38°方向700米处，则图书馆在体育馆的北偏东38°或东偏北52°方向700米处。
故答案为：B
【点睛】掌握根据方向、角度、距离确定物体位置的方法是解答题目的关键。
18. 如果a×
＝b×3（a、b都不为0），则a∶b＝（ ）。
A. 18∶5 B. 3∶
C. 5∶18
【答案】A
【解析】
【分析】假设a×
＝b×3＝1（a、b都不为0），根据分数除法的计算法则，分别求出a和b的值，再根据比的意义，求出a和b的比。
【详解】假设a×
＝b×3＝1，
a×
＝1
解：a＝1÷
a＝1×
a＝
b×3＝1
解：b＝1÷3
b＝
a∶b
＝
∶
＝（
×15）∶（
×15）
＝18∶5
故答案为：A
【点睛】此题的解题关键是利用赋值法，通过分数除法求出a和b的值，再根据比的意义，解决问题。
19. 要表示一块地各种作物占总面积的百分比，应绘制（ ）统计图更合适。
A. 条形 B. 折线 C. 扇形
【答案】C
【解析】
【分析】条形统计图可以清楚地看出数量的多少；
折线统计图不但可以表示出数量的多少，而且能够清楚地表示出数量增减变化的情况；
扇形统计图表示各部分数量与总数之间的关系。
【详解】要表示一块地各种作物占总面积的百分比，应绘制扇形统计图更合适。
故答案为：C
【点睛】理解掌握条形统计图、折线统计图、扇形统计图的特点是选择统计图的关键。
四、计算。（共29分）
20. 口算。
0×
＝ 64%－28%＝ 
÷
＝ 
÷
×
÷
＝
÷
＝ 6.8×
＝ 82－62＝ 
＋
＋
＝
【答案】0；0.36；
；25
；0.4；28；
【解析】
【详解】略
21. 计算下面各题，能简算的要简算。
（
＋
）×7×8 
0.25＋3.7×
＋3.3×25%
【答案】61；
；
；2
【解析】
【分析】（1）把7×8看作一个整体，利用乘法分配律进行简便计算；
（2）把99拆解成（100－1），再利用乘法分配律进行简便计算；
（3）先计算分数除法，再按照运算顺序从左到右依次计算；
（4）把
和25%都化成0.25，再提取相同的小数0.25，利用乘法分配律进行简便计算。
【详解】（
＋
）×7×8
＝
×7×8＋
×7×8
＝40＋21
＝61
＝
＝
＝
＝
＝
＝
＝
＝
0.25＋3.7×
＋3.3×25%
＝0.25×1＋3.7×0.25＋3.3×0.25
＝0.25×（1＋3.7＋3.3）
＝0.25×8
＝2
22. 解方程。
＋
＝
3.4
－120%
＝11 
－
＝
【答案】
＝
；
＝5；
＝
【解析】
【分析】
＋
＝
，先将左边进行合并，再根据等式的性质2解方程；
3.4
－120%
＝11，先将左边进行合并，再根据等式的性质2解方程；
－
＝
，根据等式
性质1和2，两边同时＋
，再同时×
即可。
【详解】
＋
＝
解：
＝
×
＝
×
＝
3.4
－120%
＝11
解：2.2
＝11
2.2
÷2.2＝11÷2.2
＝5
－
＝
解：
－
＋
＝
＋
×
＝
×
＝
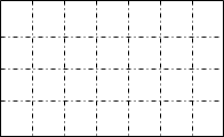
23. 在长方形格子纸中画一个最大的半圆，将剩余部分涂色，并求出涂色部分的周长和面积。（每格边长代表1米）
【答案】见详解；周长25.99米；面积8.7675平方米
【解析】
【分析】从图中可知，长方形的长是7米、宽是4米，在长方形中画一个最大的半圆，那么半圆的直径等于长方形的长7米；据此画出这个最大的半圆，并将剩余部分涂色。
观察图形可知，涂色部分的周长＝圆周长的一半＋1条长＋2条宽；涂色部分的面积＝长方形的面积－半圆的面积；根据圆的周长公式C＝πd，圆的面积公式S＝πr2，长方形的面积公式S＝ab，代入数据计算即可。
【详解】如图：
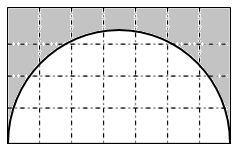
涂色部分的周长：
3.14×7÷2＋7＋4×2
＝10.99＋7＋8
＝25.99（米）
涂色部分的面积：
7×4－3.14×（7÷2）2÷2
＝28－3.14×12.25÷2
＝28－19.2325
＝8.7675（平方米）
答：涂色部分的周长是25.99米，涂色部分的面积是8.7675平方米。
【点睛】本题考查长方形内画最大的半圆，确定最大半圆的直径是画圆的关键。
求涂色部分的周长时，要弄清涂色部分是由哪些线段和曲线组成；求涂色部分的面积时，要弄清涂色部分的面积是由哪些图形相加或相减得到，然后利用相关的周长、面积公式列式计算。
六、解答题。（25分）
24. 截止2020年6月20日，中国空间技术研究院研制并成功发射
在轨工作的航天器共有608颗。
第一颗 | 第二颗 | 第三颗 | |
完成时间（年） | 41 | 6 | 3 |
完成第三颗航天器的时间比第一颗缩短了百分之几？
【答案】92.7%
【解析】
【分析】把完成第一颗航天器的时间看作单位“1”，B比A少百分之几的计算方法：（A－B）÷A×100%，完成第三颗航天器的时间比第一颗缩短的百分率＝（完成第一颗航天器的时间－完成第三颗航天器的时间）÷完成第一颗航天器的时间×100%，据此解答。
【详解】（41－3）÷41×100%
＝38÷41×100%
≈0.927×100%
＝92.7%
答：完成第三颗航天器的时间比第一颗缩短了92.7%。
【点睛】掌握一个数比另一个数少百分之几的计算方法是解答题目的关键。
25. 小明家果园共有5000m2，准备用
栽苹果树，剩下的面积按1∶4栽桃树和梨树，三种果树的面积分别是多少平方米？
【答案】苹果树1875m2；桃树625m2；梨树2500m2
【解析】
【分析】用5000×
，即可求出栽苹果树的面积；用总面积减去栽苹果树的面积即可求出栽桃树和梨树的总面积，除以总份数即可求出每份是多少平方米，再乘桃树和梨树各自对应的份数即可求出种桃树和梨树的面积。
【详解】5000×
＝1875（平方米）
（5000－1875）÷（1＋4）
＝3125÷5
＝625（平方米）
625×1＝625（平方米）
625×4＝2500（平方米）
答：苹果树1875平方米，桃树625平方米，梨树2500平方米。
【点睛】求一个数的几分之几是多少，用乘法解答；按比例分配问题，一定要先求出每份是多少。
26. 学校落实“五项管理”措施之后，宁静每天的睡眠时间达到10小时，比以前增加了
。宁静以前每天睡眠时间是多少小时？
【答案】
小时
【解析】
【分析】把以前的睡眠时间看作单位“1”，那么现在的睡眠时间是以前的（1＋
），现在的睡眠时间÷（1＋
），即可求出以前每天的睡眠时间。
【详解】10÷（1＋
）
＝10÷
＝
（小时）
答：宁静以前每天睡眠时间是
小时。
【点睛】此题考查了分数
四则混合运算，找准单位“1”，明确求单位“1”用除法。
27. 为进一步提升老百姓生活的幸福指数，政府拟对一个老旧小区进行提升改造。甲工程队单独完成这项工程需要70天，乙工程队每天可以完成这项工程的
。如果甲乙两个工程队合作，需要多少天可以完成这项工程的
？
【答案】
天
【解析】
【分析】把这项工程看作单位“1”，甲工程队每天可以完成这项工程的1÷70＝
，用工作时间＝工作总量÷工作效率之和，用
除以两个小队的工作效率之和，即可求出合作的时间。
【详解】1÷70＝
÷（
＋
）
＝
÷
＝
×
＝
（天）
答：需要
天可以完成这项工程的
。
【点睛】此题考查了工程问题，先表示出甲工程队的工作效率是解题关键。
28. 我国的国土地面积约为960万平方千米，各种地形所占百分比如图。
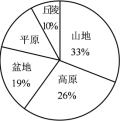
（1）平原面积占国土面积的百分比是多少？
（2）丘陵面积和山地面积一共是多少万平方千米？
【答案】（1）12%
（2）412.8万平方千米
【解析】
【分析】（1）把我国的国土面积看作单位“1”，根据减法的意义，用“1”减去丘陵、山地、高原、盆地占国土面积的百分比之和，就是平原面积占国土面积的百分比。
（2）把我国的国土面积看作单位“1”，丘陵面积和山地面积一共占国土面积的（10%＋33%），根据求一个数的百分之几是多少，用乘法计算即可求解。
【详解】（1）1－（10%＋33%＋26%＋19%）
＝1－88%
＝12%
答：平原面积占国土面积的12%。
（2）960×（10%＋33%）
＝960×0.43
＝412.8（万平方千米）
答：丘陵面积和山地面积一共是412.8万平方千米。
【点睛】掌握扇形统计图的特点及作用，从中获取信息，根据统计图提供的信息解决有关的百分数问题。