2022年北京海淀高一数学下学期期末试卷及答案
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知正四棱锥的底面边长为2,高为3,则它的体积为![]()
![]()
A.2 B.4 C.6 D.12
2.向量![]() ,
,![]() ,则
,则![]()
![]()
A.![]() B.
B.![]() C.4 D.13
C.4 D.13
3.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象,则
的图象,则![]() 的最小值是
的最小值是![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知直线![]() 和平面
和平面![]() ,
,![]() ,则下列四个命题中正确的是
,则下列四个命题中正确的是![]()
![]()
A.若![]() ,
,![]() ,则
,则![]() B.若
B.若![]() ,
,![]() ,则
,则![]()
C.若![]() ,
,![]() ,则
,则![]() D.若
D.若![]() ,
,![]() ,则
,则![]()
6.函数![]() 的最小正周期与其图象的对称中心分别是
的最小正周期与其图象的对称中心分别是![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.已知向量![]() ,
,![]() 是两个单位向量,则“
是两个单位向量,则“![]() ,
,![]() 为锐角”是“
为锐角”是“![]() ”的
”的![]()
![]()
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
8.已知函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,则
,则![]() 的取值范围是
的取值范围是![]()
![]()
A.![]() B.
B.![]()
C.![]() ,
,![]() ,
,![]() D.
D.![]()
9.底与腰(或腰与底)之比为黄金分割比![]() 的等腰三角形称为黄金三角形,其中顶
的等腰三角形称为黄金三角形,其中顶
角为![]() 的黄金三角形被认为是最美的三角形.据此可得
的黄金三角形被认为是最美的三角形.据此可得![]() 的值是
的值是![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.在![]() 中,
中,![]() ,则
,则![]() 的形状是
的形状是![]()
![]()
A.等腰直角三角形 B.等腰三角形
C.直角三角形 D.等腰三角形或直角三角形
二、填空题共5小题,每小题4分,共20分。
11.已知圆柱的底面半径为1,高为2,则其侧面积为 .
12.向量![]() ,
,![]() ,
,![]() ,则实数
,则实数![]() .
.
13.在正方形![]() 中,
中,![]() 是
是![]() 的中点,则
的中点,则![]() .
.
14.函数![]() ,
,![]() 的值域是 .
的值域是 .
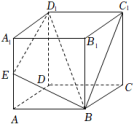 15.如图,在棱长为1的正方体
15.如图,在棱长为1的正方体![]() 中,
中,![]() 是棱
是棱![]() 上的一个动点,给出下列四个结论:
上的一个动点,给出下列四个结论:
①三棱锥![]() 的体积为定值;
的体积为定值;
②存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
③对每一个点![]() ,在棱
,在棱![]() 上总存在一点
上总存在一点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 的截面
的截面![]() 垂直于
垂直于![]() ,则截面
,则截面![]() 的面积的最小值为
的面积的最小值为![]() .
.
其中所有正确结论的序号是 .
三、解答题共4小题,共40分。解答应写出文字说明、演算步骤或证明过程。
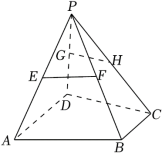
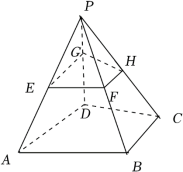
16.(9分)如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() ,
,![]() ,
,![]() 的中点,
的中点,
(Ⅰ)求证:![]() ;
;
(Ⅱ)判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
17.(10分)在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求![]() ;
;
(Ⅱ)求![]() 的面积.
的面积.
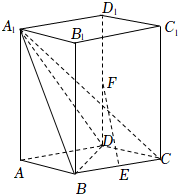
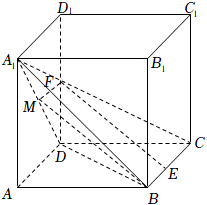
18.(11分)如图,在直棱柱![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点.
的中点.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)是否存在正数![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
19.(10分)若点![]() ,
,![]() 在函数
在函数![]() 的图象上,且满足
的图象上,且满足![]() ,则称
,则称![]() 是
是![]() 的
的![]() 点.函数
点.函数![]() 的所有
的所有![]() 点构成的集合称为
点构成的集合称为![]() 的
的![]() 集.
集.
(Ⅰ)判断![]() 是否是函数
是否是函数![]() 的
的![]() 点,并说明理由;
点,并说明理由;
(Ⅱ)若函数![]() 的
的![]() 集为
集为![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)若定义域为![]() 的连续函数
的连续函数![]() 的
的![]() 集
集![]() 满足
满足![]() ,求证:
,求证:![]() .
.
选做题:(本题满分0分。所得分数可计人总分,但整份试卷得分不超过100分)
20.正弦信号是频率成分最为单一的信号,复杂的信号,例如电信号,都可以分解为许多频率不同、幅度不等的正弦型信号的叠加.正弦信号的波形可以用数学上的正弦型函数来描述:![]() ,其中
,其中![]() 表示正弦信号的瞬时大小电压
表示正弦信号的瞬时大小电压![]() (单位:
(单位:![]() 是关于时间
是关于时间![]() (单位:
(单位:![]() 的函数,而
的函数,而![]() 表示正弦信号的幅度,
表示正弦信号的幅度,![]() 是正弦信号的频率,相应的
是正弦信号的频率,相应的![]() 为正弦信号的周期,
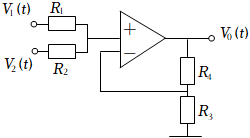
为正弦信号的周期,![]() 为正弦信号的初相.由于正弦信号是一种最简单的信号,所以在电路系统设计中,科学家和工程师们经常以正弦信号作为信号源(输入信号)去研究整个电路的工作机理.如图是一种典型的加法器电路图,图中的三角形图标是一个运算放大器,电路中有四个电阻,电阻值分别为
为正弦信号的初相.由于正弦信号是一种最简单的信号,所以在电路系统设计中,科学家和工程师们经常以正弦信号作为信号源(输入信号)去研究整个电路的工作机理.如图是一种典型的加法器电路图,图中的三角形图标是一个运算放大器,电路中有四个电阻,电阻值分别为![]() ,
,![]() ,
,![]() ,
,![]() (单位:
(单位:![]() 和
和![]() 是两个输入信号,
是两个输入信号,![]() 表示的是输出信号,根据加法器的工作原理,
表示的是输出信号,根据加法器的工作原理,![]() 与
与![]() 和
和![]() 的关系为:
的关系为:![]() .
.
例如当![]() ,输入信号
,输入信号![]() ,
,![]() 时,输出信号:
时,输出信号:![]() .
.
(Ⅰ)若![]() ,输入信号
,输入信号![]() ,
,![]() ,则
,则![]() 的最大值为 ;
的最大值为 ;
(Ⅱ)已知![]() ,
,![]() ,
,![]() ,输入信号
,输入信号![]() ,
,![]() .若
.若![]() (其中
(其中![]() 则
则![]() ;
;
(Ⅲ)已知![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .若
.若![]() 的最大值为
的最大值为![]() ,则满足条件的一组电阻值
,则满足条件的一组电阻值![]() ,
,![]() 分别是 .
分别是 .
参考答案
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
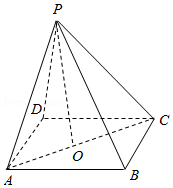
1.解:如图,正四棱锥![]() 中,
中,![]() ,
,![]() ,
,
所以![]() .
.
故选:![]() .
.
考查数形结合思想等,是中档题.
2.解:因为向量![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() .
.
故选:![]() .
.
3.解:将将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后,
个单位长度后,
得到函数![]() ,
,
所以![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() .
.
故选:![]() .
.
4.解:![]() .
.
故选:![]() .
.
5.解:对于![]() 选项,若
选项,若![]() ,
,![]() ,则
,则![]() 可能与
可能与![]() 平行,故
平行,故![]() 错误;
错误;
对于![]() 选项,若
选项,若![]() ,
,![]() ,则
,则![]() ,
,![]() 可能平行或者相交,则
可能平行或者相交,则![]() 错误;
错误;
对于![]() 选项,若
选项,若![]() ,
,![]() ,则
,则![]() 可能与
可能与![]() 平行或者在平面
平行或者在平面![]() 内,故
内,故![]() 错误;
错误;
对于![]() 选项,由面面平行以及线面垂直的性质可知,
选项,由面面平行以及线面垂直的性质可知,![]() 正确;
正确;
故选:![]() .
.
6.解:因为![]() ,
,
所以函数的最小正周期为![]() ,
,
令![]() ,
,![]() ,解得
,解得![]() ,
,
所以函数的对称中心为![]() ,
,![]() ,
,![]() ,
,
故选:![]() .
.
7.解:![]() 向量
向量![]() ,
,![]() 是两个单位向量,
是两个单位向量,
![]() 由
由![]() ,
,![]() 为锐角可得
为锐角可得![]() ,
,
![]()
![]() ,
,
反过来,由![]() 两边平方可得
两边平方可得![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() 不一定为锐角,
不一定为锐角,
故“![]() ,
,![]() 为锐角”是“
为锐角”是“![]() ”的充分不必要条件,
”的充分不必要条件,
故选:![]() .
.
【点评】本题考查充分与必要条件的概念,平面向量数量积的定义与性质,属基础题.
8.【分析】先根据![]() 的范围求出
的范围求出![]() 的范围,根据函数
的范围,根据函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,可得到
,可得到![]() ,即
,即![]() ,然后对
,然后对![]() 分大于0和小于0两种情况讨论最值可确定答案.
分大于0和小于0两种情况讨论最值可确定答案.
【解答】解:当![]() 时,
时,![]() ,
,
由题意知![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,
,
由题意知![]() ,即
,即![]() ,
,
综上知,![]() 的取值范围是
的取值范围是![]() .
.
故选:![]() .
.
9.解:由题意可知:把顶角为![]() 的等腰三角形称为黄金三角形,它的底和腰之比为黄金分割比
的等腰三角形称为黄金三角形,它的底和腰之比为黄金分割比![]() ,该三角形被认为是最美的三角形.
,该三角形被认为是最美的三角形.
如图,则可得: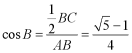 ,
,
可得![]() ,
,![]()
即![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() .
.
故选:![]() .
.
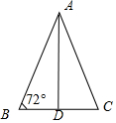
10.解:利用正弦定理:![]() 转换为
转换为![]() ,
,
整理得![]() ,
,
故![]() 或
或![]() ;
;
所以![]() 或
或![]() ;
;
故三角形为等腰三角形或直角三角形.
故选:![]() .
.
二、填空题共5小题,每小题4分,共20分。
11.解:圆柱的底面半径为1,高为2,
则其侧面积为![]() .
.
故答案为:![]() .
.
12.解:![]() ,
,![]() ,
,
![]()
![]() ,解得
,解得![]() .
.
故答案为:![]() .
.
13.解:如图![]() ,
,
因为![]() ,所以
,所以![]() ;
;
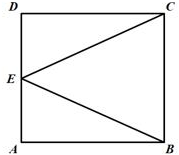
故答案为:0.
14解:![]() ;
;
由于![]() ,
,
所以![]() ,
,
故![]() .
.
故答案为:![]() .
.
15.解:对于①,如图,在棱长为1的正方体![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 点
点![]() 是棱
是棱![]() 上的一个动点,
上的一个动点,![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
![]() ,
,
![]() 三棱锥
三棱锥![]() 的体积
的体积![]() ,故①正确;
,故①正确;
对于②,当![]() 为棱
为棱![]() 的中点时,取
的中点时,取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,如图,
,如图,
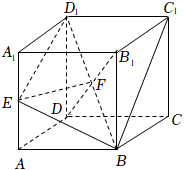
则![]() ,又
,又![]() ,
,![]() ,
,![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() ,
,
由正方体性质得![]() 是矩形,不是正方体,
是矩形,不是正方体,
![]() 不成立,又
不成立,又![]() ,
,
![]() 不存在点
不存在点![]() ,使得
,使得![]() 平面
平面![]() ,故②错误;
,故②错误;
对于③,当![]() 与点
与点![]() 重合时,无论点
重合时,无论点![]() 在何位置,直线
在何位置,直线![]() 与平面
与平面![]() 相交,故③错误;
相交,故③错误;
对于④,根据题意,作图如下,
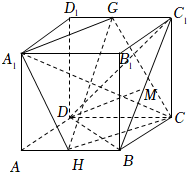
![]() 正方体
正方体![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
则△![]() 中,
中,![]() ,
,
![]() ,
,
则该截面面积![]() ,
,
![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,故④正确.
,故④正确.
故答案为:①④.
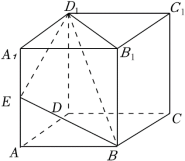
【点评】本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.
三、解答题共4小题,共40分。解答应写出文字说明、演算步骤或证明过程。
16.证明:![]() 因为
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() .
.
证明:![]() 直线
直线![]() 与直线
与直线![]() 相交.理由如下:
相交.理由如下:
连接![]() ,
,![]() ,
,![]() ,
,![]() ,如图所示,
,如图所示,
因为![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,所以
的中点,所以![]() 是
是![]() 的中位线,所以
的中位线,所以![]() ,且
,且![]() ,
,
因为![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,所以
的中点,所以![]() 是
是![]() 的中位线,
的中位线,
所以![]() ,且
,且![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以四边形![]() 是梯形,
是梯形,
所以直线![]() 与直线
与直线![]() 相交.
相交.
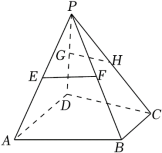
17.解:(Ⅰ)由正弦定理可得,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(Ⅱ)![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
18.![]() 证明:如图,连接
证明:如图,连接![]() ,因为底面
,因为底面![]() 是菱形,
是菱形,
所以![]() ,直棱柱
,直棱柱![]() 中,
中,![]() 平面
平面![]() ,
,
所以![]() ,且
,且![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() ;
;

![]() 证明:取
证明:取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() 为三角形
为三角形![]() 的中位线,
的中位线,
所以![]() 且
且![]() ,又因为
,又因为![]() 且
且![]() ,
,
又![]() 且
且![]() ,所以
,所以![]() 且
且![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
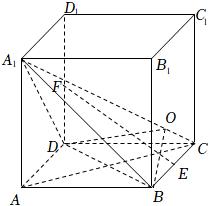
解:![]() 不存在正数
不存在正数![]() ,使得平面
,使得平面![]() 平面
平面![]() ,证明如下:
,证明如下:
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
在直角△![]() 中,
中,![]() ,所以
,所以![]() ,
,
假设存在正数![]() ,使得平面
,使得平面![]() 平面
平面![]() ,如图,
,如图,
过![]() 作
作![]() 且与
且与![]() 交于
交于![]() 点,连接
点,连接![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() ,在直角△
,在直角△![]() 中,
中,![]() ,同理
,同理![]() ,
,
因为底面![]() 是菱形,
是菱形,![]() ,
,![]() ,所以
,所以![]() ,
,
在直角三角形![]() 中,
中,![]() ,得
,得![]() ,
,
化简得![]() 与已知
与已知![]() 为正数矛盾,所以不存在正数
为正数矛盾,所以不存在正数![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
19.解:![]() 不是函数
不是函数![]() 的点,
的点,
理由如下:设![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() 不是函数
不是函数![]() 的
的![]() 点;
点;
![]() 先证明
先证明![]() ,若
,若![]() ,则函数
,则函数![]() 的最小正周期
的最小正周期![]() ,
,
因为函数![]() 的集为
的集为![]() ,
,
所以对![]() ,
,![]() 是
是![]() 的零点,
的零点,
令![]() ,则
,则![]() ,
,
因为函数![]() 的值域为
的值域为![]() ,
,![]() ,
,
所以当![]() ,
,![]() 时,必有
时,必有![]() ,
,
即![]() 对于
对于![]() ,
,![]() 恒成立,
恒成立,
所以![]() ,即
,即![]() 的最小正周期
的最小正周期![]() ,与
,与![]() 矛盾;
矛盾;
再证明![]() 的值可以等于
的值可以等于![]() ,令
,令![]() ,对
,对![]() ,
,
当![]() ,
,![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;
当![]() ,
,![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
所以![]() 是
是![]() 的点,即函数
的点,即函数![]() 的集为
的集为![]() ,
,
综上所述,![]() 的最大值是
的最大值是![]() ;
;
![]() 因为函数
因为函数![]() 的集
的集![]() 满足
满足![]() ,
,
所以存在![]() ,使得
,使得![]() 且
且![]() ,即
,即![]() ,
,
因为若![]() ,则
,则![]() ,所以
,所以![]() ,
,
因为函数![]() 的图象是连续不断的,
的图象是连续不断的,
不妨设![]() ,由零点存在定理知,必存在
,由零点存在定理知,必存在![]() ,
,![]() 使得
使得![]() ,
,
所以![]() 存在零点,
存在零点,
即![]() .
.
选做题:(本题满分0分。所得分数可计人总分,但整份试卷得分不超过100分)
20.解:(Ⅰ)由题意得,![]() ,则
,则![]() 的最大值为
的最大值为![]() ;
;
(Ⅱ)由题意知, ,
,
整理得![]() ,
,
即![]() ,
,
则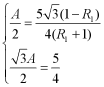 ,解得
,解得![]() ;
;
(Ⅲ)由题意得,![]()
![]() ,
,
又![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,
,
则![]() ,整理得
,整理得![]() ,
,
即![]() ,解得
,解得![]() ,
,
又![]() ,则
,则![]() ,
,
取![]() 即满足题意,
即满足题意,
则![]() (答案不唯一).
(答案不唯一).
故答案为:![]() ;
;![]() ;
;![]() .
.